Oto tytuły i streszczenia seminariów z 2014 roku:
2014-12-09 Seminarium nieliniowe
Monika Naskręcka
Istnienie rozwiązania pewnego szczególnego układu równań różniczkowych z nieciągłą prawą stroną
Podczas seminarium omówimy dowód istnienia rozwiązania pewnego układu równań różniczkowych z prawą stroną nieciągłą. Układ ten opisuje dynamikę zapasów w modelu gospodarki konkurencyjnej.
2014-12-02 Seminarium nieliniowe
Marcin Borkowski
O pewnym twierdzeniu o punkcie stałym w przestrzeniach
ultrametrycznych
(Kontynuacja seminarium z 2014-11-18 oraz 2014-11-04)
2014-11-25 Seminarium nieliniowe
dr Przemysław Chełminiak
Dynamika stochastyczna na samoorganizujących się sieciach krytycznych
Samoorganizujące się sieci krytyczne są przedmiotem intensywnych badań od przeszło piętnastu lat. Cechuje je szereg osobliwych własności, takich jak bezskalowość, efekt małych światów, fraktalność, samopodobieństwo oraz topologiczna krytyczność, wynikających z reguł leżących u podstaw ich stochastycznej ewolucji. Okazuje się, że wiele z tych sieci istnieje w stanie niestabilnym na granicy dwóch faz, fraktal-mały świat. Przedstawione zostaną metody analizy i konstrukcji sieci krytycznych, oraz podstawowe własności rozkładów prawdopodobieństw strumieni stacjonarnych wynikających z dynamiki stochastycznej na tych sieciach.
2014-11-18 Seminarium nieliniowe
Marcin Borkowski
O pewnym twierdzeniu o punkcie stałym w przestrzeniach
ultrametrycznych
(Kontynuacja seminarium z 2014-11-04)
2014-11-04 Seminarium nieliniowe
O pewnym twierdzeniu o punkcie stałym w przestrzeniach
ultrametrycznych
Podczas referatu omówimy pewien wariant twierdzenia Banacha o kontrakcji (pochodzący od N. Ackermana) dla przestrzeni ultrametrycznych z metryką o wartościach w kracie zupełnej.
2014-10-28 Seminarium nieliniowe
Dr Mateusz Maciejewski
Istnienie dodatnich rozwiązań układu równań parabolicznych z nielokalnymi warunkami początkowymi
Tematem odczytu jest istnienie dodatnich rozwiązań układów równań parabolicznych z warunkami brzegowymi Dirichleta i z nielokalnymi warunkami początkowymi. W tym celu przedstawię twierdzenie o punkcie stałym, którego dowód opiera się na indeksie punktów stałych Granasa. Dzięki możliwości lokalizowania rozwiązań, otrzymam twierdzenia o istnieniu więcej niż jednego rozwiązania.
2014-10-21 Seminarium nieliniowe
Marcin Borkowski
Twierdzenia o punktach stałych z warunkiem brzegowym
2014-10-14 Seminarium nieliniowe
Piotr Kasprzak
Gra Hex i twierdzenie Brouwera o punkcie stałym.
Podczas seminarium wykażemy, że twierdznie Brouwera o punkcie stałym jest konsekwencją faktu, iż gra Hex nie może zakończyć się remisem.
2014-10-07 Seminarium nieliniowe
Marcin Borkowski
Twierdzenia o punktach stałych z warunkiem brzegowym
W 1998 roku Espínola i López udowodnili pewne twierdzenie o punkcie stałym dla odwzorowania działającego z dopuszczalnego podzbioru 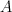 przestrzeni metrycznej hiperwypukłej w całą tę przestrzeń, przy założeniu, że odwzorowanie to przekształca brzeg zbioru
przestrzeni metrycznej hiperwypukłej w całą tę przestrzeń, przy założeniu, że odwzorowanie to przekształca brzeg zbioru 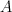 w ten zbiór. Pokażemy, jak można znacząco uprościć dowód głównego lematu z ich pracy, zarazem znacząco osłabiając jego założenia. W szczególności, umożliwi to podanie nowego twierdzenia o punkcie stałym, uogólniającego klasyczny wynik Baillona z 1988 roku.
w ten zbiór. Pokażemy, jak można znacząco uprościć dowód głównego lematu z ich pracy, zarazem znacząco osłabiając jego założenia. W szczególności, umożliwi to podanie nowego twierdzenia o punkcie stałym, uogólniającego klasyczny wynik Baillona z 1988 roku.
2014-09-30 Seminarium nieliniowe
prof. Gennaro Infante
Nietrywialne rozwiązania równań całkowych Hammersteina z zaburzeniem
Omówimy istnienie dodatnich rozwiązań pewnych równań całkowych Hammersteina z zaburzeniem w ujęciu klasycznej teorii punktów stałych. Użyjemy naszych wyników do pewnych nielokalnych BVP, które występują w pewnych zagadnieniach przepływu ciepła, by udowodnić istnienie wielu dodatnich rozwiązań, przy odpowiednich założeniach. Zilustrujemy również w jaki sposób to podejście może zostać zaaplikowane do różnych problemów.
2014-09-16 Seminarium nieliniowe
Dariusz Bugajewski
BV-rozwiązania równań nieliniowych
Podczas seminarium udowodnimy istnienie rozwiązań BV pewnych równań nieliniowych przy użyciu twierdzeń o punktach stałych.
2014-06-10 Seminarium nieliniowe
Adam Nawrocki
Operator splotu określony na przestrzeni funkcji
prawie okresowych w sensie Lewitana
(Kontynuacja seminarium z 2014-05-27)
2014-05-27 Seminarium nieliniowe
Adam Nawrocki
Operator splotu określony na przestrzeni funkcji
prawie okresowych w sensie Lewitana
Wiadomo, że splot ograniczonej funkcji prawie okresowej w sensie Lewitana z funkcją 202424.png) jest funkcją prawie okresową w sensie Lewitana. W referacie zastanowimy się nad rezultatem jaki otrzymamy rozważając nieograniczone funkcje prawie okresowe w sensie Lewitana.
jest funkcją prawie okresową w sensie Lewitana. W referacie zastanowimy się nad rezultatem jaki otrzymamy rozważając nieograniczone funkcje prawie okresowe w sensie Lewitana.
2014-05-20 Seminarium nieliniowe
Adam Nawrocki
Asymptotyczne zachowanie pewnej funkcji prawie okresowej wzgledem miary Lebesgue'a
Funkcja
3d5cfrac7b17d7b22b5ccos20x202b5ccos7b(x5csqrt202)7d7d0a205cend7bdisplaymath7d.png) (1)
(1)jest klasycznym przykładem nieograniczonej i ciągłej funkcji
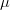 -prawie okresowej. Dla tej funkcji zachodzi
-prawie okresowej. Dla tej funkcji zachodzi7d7d3d0.0a205cend7bdisplaymath7d.png) (2)
(2)W referacie omówimy ideę dowodu powyższej równości, w której wykorzystuje się aproksymacje diofantyczne. Pokażemy ponadto, że granica
7d7d0a205cend7bdisplaymath7d.png) (3)
(3)nie istnieje.
2014-05-06 Seminarium nieliniowe
Monika Naskręcka
Matematyczny model gospodarki konkurencyjnej z zapasami
(Kontynuacja seminarium z 2014-04-29, 2014-03-25, 2014-01-28,
2014-01-21, 2013-11-05 oraz 2013-10-29)
2014-04-29 Seminarium nieliniowe
Monika Naskręcka
Matematyczny model gospodarki konkurencyjnej z zapasami
(Kontynuacja seminarium z 2014-03-25, 2014-01-28,
2014-01-21, 2013-11-05 oraz 2013-10-29)
2014-04-15 Seminarium nieliniowe
Adam Nawrocki
Asymptotyczne zachowanie pewnych funkcji 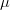 -prawie okresowych
-prawie okresowych
Funkcja
3d5cfrac7b17d7b22b5ccos20x202b5ccos7b(x5csqrt202)7d7d0a205cend7bdisplaymath7d.png) (4)
(4)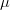 -prawie okresowej. Dla tej funkcji zachodzi
-prawie okresowej. Dla tej funkcji zachodzi7d7d3d0.0a205cend7bdisplaymath7d.png) (5)
(5)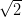 na inną liczbę niewymierną może znacząco wpłynąć na zachowanie funkcji. Skonstruujemy liczbę niewymierną
na inną liczbę niewymierną może znacząco wpłynąć na zachowanie funkcji. Skonstruujemy liczbę niewymierną 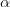 taką, że granica
taką, że granica7d7d0a205cend7bdisplaymath7d.png) (6)
(6)Referat zostanie poprzedzony krótkim komunikatem, który wygłosi Marcin Borkowski.
2014-04-01 Seminarium nieliniowe
dr Michał Goliński
O pewnych własnościach przestrzeni funkcji prawie okresowych
Na seminarium omówimy pewne własności przestrzeni 202424.png) funkcji prawie okresowych, ze szczególnym uwzględnieniem własności topologii słabej (ciągi Cauchy'ego, zupełność, refleksywność).
funkcji prawie okresowych, ze szczególnym uwzględnieniem własności topologii słabej (ciągi Cauchy'ego, zupełność, refleksywność).
2014-03-25 Seminarium nieliniowe
Monika Naskręcka
Matematyczny model gospodarki konkurencyjnej z zapasami
(Kontynuacja seminarium z 2013-10-29 oraz 2013-11-05)
2014-03-18 Seminarium nieliniowe
Marcin Borkowski
O pewnym zastosowaniu twierdzenia Möncha
(Kontynuacja seminarium z 2014-02-25 oraz 2014-03-04)
2014-03-11 Seminarium nieliniowe
Dr Jacek Gulgowski
(Instytut Matematyki, Uniwersytet Gdański)
O ciągłości operatora superpozycji w przestrzeniach funkcji o ograniczonej wariacji
Wiadomo, że funkcja ciągła 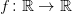 , spełniająca lokalny warunek Lipschitza, złożona z funkcją
, spełniająca lokalny warunek Lipschitza, złożona z funkcją 202424.png) o ograniczonej wariacji daje również funkcję
o ograniczonej wariacji daje również funkcję (t)202424.png) o ograniczonej wariacji. W naturalny sposób pojawia się w tym miejscu pytanie o ciągłość takiego operatora superpozycji
o ograniczonej wariacji. W naturalny sposób pojawia się w tym miejscu pytanie o ciągłość takiego operatora superpozycji ![$$ F \colon BV[0,1]\to BV[0,1] $$](https://octd.wmi.amu.edu.pl/latex/242420F205ccolon20BV5b02c15d5cto20BV5b02c15d202424.png) . Omówione zostaną pewne przypadki, w których można pokazać, że wspomniany operator jest ciągły. Podane zostaną również pewne znane uogólnienia pojęcia wariacji funkcji prowadzące do definicji przestrzeni Banacha
. Omówione zostaną pewne przypadki, w których można pokazać, że wspomniany operator jest ciągły. Podane zostaną również pewne znane uogólnienia pojęcia wariacji funkcji prowadzące do definicji przestrzeni Banacha 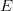 zawierających przestrzeń
zawierających przestrzeń ![$$ BV[0,1] $$](https://octd.wmi.amu.edu.pl/latex/242420BV5b02c15d202424.png) . W pewnych sytuacjach można również pokazać ciągłość operatora superpozycji
. W pewnych sytuacjach można również pokazać ciągłość operatora superpozycji ![$$ F \colon BV[0,1]\to E $$](https://octd.wmi.amu.edu.pl/latex/242420F205ccolon20BV5b02c15d5cto20E202424.png) .
.
2014-03-04 Seminarium nieliniowe
Marcin Borkowski
O pewnym zastosowaniu twierdzenia Möncha
(Kontynuacja seminarium z 2014-02-25)
2014-02-25 Seminarium nieliniowe
Marcin Borkowski
O pewnym zastosowaniu twierdzenia Möncha
Przedmiotem referatu będzie zastosowanie twierdzenia Möncha o punkcie
stałym do pewnego zagadnienia II rzędu z warunkami brzegowymi typu
Sturma–Liouville'a..
2014-01-28 Seminarium nieliniowe
Marcin Karczewski
Równanie kinetyczne Boltzmanna
Podsumowane zostaną seminaria z 2013-12-10 oraz 2013-12-17.
oraz
Monika Naskręcka
Matematyczny model gospodarki konkurencyjnej z zapasami
(Kontynuacja seminarium z 2013-10-29, 2013-11-05 oraz 2014-01-21)
2014-01-21 Seminarium nieliniowe
Monika Naskręcka
Matematyczny model gospodarki konkurencyjnej z zapasami
(Kontynuacja seminarium z 2013-10-29 oraz 2013-11-05)
2014-01-14 Seminarium nieliniowe
prof. UW dr hab. Urszula Foryś (Uniwersytet Warszawski)
Modelowanie reakcji biochemicznych z opóźnieniem
Od pewnego czasu w opisie reakcji biochemicznych zaczęto stosować nie tylko równania różniczkowe zwyczajne, ale też równania z opóźnionym argumentem. Wprowadzenie opóźnienia ma na celu uwzględnienie różnych skal czasowych, w jakich zachodzą rozważane reakcje. W trakcie naszych (wraz z M. Bodnarem, J. Miękiszem i J. Poleszczukiem) prac przekonaliśmy się, że proste, wydawałoby się ,,intuicyjne” metody wprowadzenia opóźnienia prowadzą do niewłaściwych wniosków, w szczególności do wniosku, że w prostej reakcji opóźnionej degradacji białka możliwe są oscylacje. Uzasadnię, że najprostszy model, zaproponowany przez Bratsuna i in. (2005), jest niewłaściwy i pokażę, w jaki sposób należy go zmodyfikować. Okazuje się, że dopiero w przypadku znacznie bardziej skomplikowanej reakcji ze sprzężeniem zwrotnym i dimeryzacją mogą wystąpić oscylacje.
Seminarium wyjątkowo odbędzie się w sali B1-37.
2014-01-07 Seminarium nieliniowe
dr Aneta Sikorska-Nowak
Nieliniowe równanie dynamiczne Sturm-Liouville’a
Zaprezentowane zostaną niezbędne pojęcia dotyczące równań dynamicznych na skalach czasowych oraz nieliniowe równanie dynamiczne Sturm-Liouville’a.