Oto tytuły i streszczenia seminariów z 2015 roku:
2015-12-15 Seminarium nieliniowe
Marcin Borkowski
O pewnym twierdzeniu o punkcie stałym w przestrzeniach ultrametrycznych
Podczas referatu omówimy twierdzenie gwarantujące istnienie punktu stałego oraz (uogólnionego) ciągu aproksymującego ten punkt stały. Referat oparty jest na pracy S. Priess-Crampe i P. Ribenboima z 2013 roku.
2015-12-08 Seminarium nieliniowe
Mateusz Krukowski
Twierdzenie typu Darbo dla quasimiar niezwartości
Prezentacja wprowadza pojęcie quasimiary niezwartości. Funkcje te nie muszą być niezmiennicze na wypukłe otoczki, w przeciwieństwie do klasycznych miar niezwartości. Z pomocą kryterium zwartości w przestrzeni 202424.png) (
(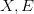 to przestrzenie Banacha, gdzie
to przestrzenie Banacha, gdzie 203c205cinfty202424.png) ), konstruujemy quasimiarę niezwartości i badamy jej właściwości. Ponadto, dowodzimy analogon twierdzenia Darbo przy pomocy miary niewypukłości. Pokazujemy także sposób wykorzystania przed- stawionych narzędzi do znajdywania punktu stałego operatora Hammersteina.
), konstruujemy quasimiarę niezwartości i badamy jej właściwości. Ponadto, dowodzimy analogon twierdzenia Darbo przy pomocy miary niewypukłości. Pokazujemy także sposób wykorzystania przed- stawionych narzędzi do znajdywania punktu stałego operatora Hammersteina.
2015-12-01 Seminarium nieliniowe
Paweł Kliber
Wybór konsumenta stosującego dyskontowanie hiperboliczne - model i warunki Eulera
(Kontynuacja seminarium z 2015-11-17)
2015-11-17 Seminarium nieliniowe
Paweł Kliber
Wybór konsumenta stosującego dyskontowanie hiperboliczne - model i warunki Eulera
(Kontynuacja seminarium z 2015-10-20, 2015-11-03 oraz 2015-11-10 Seminarium nieliniowe.)
2015-11-10 Seminarium nieliniowe
Paweł Kliber
Wybór konsumenta stosującego dyskontowanie hiperboliczne - model i warunki Eulera
(Kontynuacja seminarium z 2015-10-20 oraz 2015-10-27.)
2015-11-03 Seminarium nieliniowe
Paweł Kliber
Wybór konsumenta stosującego dyskontowanie hiperboliczne - model i warunki Eulera
(Kontynuacja seminarium z 2015-10-20.)
2015-10-27 Seminarium nieliniowe
Elżbieta Gajecka
Metody resamplingowe w dziedzinie czasu dla szeregów czasowych o strukturze okresowej i prawie okresowej
(Seminarium odbędzie się w sali B3-38)
Wnioskowanie statystyczne, w przypadku szeregów czasowych, oparte na rozkładach asymptotycznych nie zawsze może być podstawę efektywnych procedur statystycznych. Jednak nieznane rozkłady estymatorów lub statystyk mogę być przybliżać bezpośrednio za pomoc tzw. procedur resamplingowych.
Ideą metod resamplingowych jest otrzymywanie replikacji estymatora, a następnie obliczanie z tych replikacji rozkładu empirycznego. Podstawowym pytaniem, na które trzeba odpowiedzieć to czy ten rozkład empiryczny, zwany rozkładem resamplingowym, jest bliski prawdziwemu rozkładowi. Prowadzone są intensywne badania w zakresie metod resamplingowych dla niestacjonarnych szeregów czasowych, w szczegolności szeregów o strukturze okresowej i prawie okresowej.
W prezentacji przedstawione zostaną różne sposoby resamplingowania, w szczególności sub-sampling. Zaletą subsamplingu jest jego niewrażliwo na postać rozkladu asymptotycznego. Przedstawione zostaną również warunki zgodności metod resamplingowych w dziedzinie czasu dla 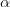 −mieszających albo słabo zależnych szeregów czasowych o strukturze okresowej i prawie okresowej. Szczególnie słaba zależność daje nowe narzędzia do analizy procedur statystycznych dla bardzo ogólnych danych generujących szeregi czasowe, także dla szeregów okresowych o długiej pamięci i ciężkich ogonach. Przedstawiony zostanie przykład modelu okresowego z ciężkimi ogonami i długą pamięcią.
−mieszających albo słabo zależnych szeregów czasowych o strukturze okresowej i prawie okresowej. Szczególnie słaba zależność daje nowe narzędzia do analizy procedur statystycznych dla bardzo ogólnych danych generujących szeregi czasowe, także dla szeregów okresowych o długiej pamięci i ciężkich ogonach. Przedstawiony zostanie przykład modelu okresowego z ciężkimi ogonami i długą pamięcią.
2015-10-20 Seminarium nieliniowe
Paweł Kliber
Wybór konsumenta stosującego dyskontowanie hiperboliczne - model i warunki Eulera
Prezentacja dotyczy artykułu, w którym rozważany jest problem wyboru ścieżki konsumpcji w czasie dla konsumenta stosującego dyskontowanie hiperboliczne (inaczej traktuje chwilę obecną, a inaczej całą przyszłość) w modelu z losowymi stopami zwrotu z inwestycji. Przedstawiony jest model i jego założenia oraz najważniejsze własności rozwiązania.
2015-10-13 Seminarium nieliniowe
Piotr Kasprzak
Całkowe równanie Abela
(Kontynuacja seminarium z 2015-10-06.)
2015-10-06 Seminarium nieliniowe
Piotr Kasprzak
Całkowe równanie Abela
Celem seminarium będzie omówienie podstawowych zagadnień
teoretycznych dotyczących całkowego równania Abela, a także zaprezentowanie przykładowych zastosowań fizycznych tego równania.
2015-06-09 Seminarium nieliniowe
Adam Nawrocki
Funkcje dwuokresowe
(Kontynuacja seminarium z 2015-04-28)
2015-06-02 Seminarium nieliniowe
Prof. Xiao-Xiong Gan
(Mathematics Department, Morgan State University, Baltimore, USA)
Some Remarks on Minkowski's Inequality
The classical Minkowski's inequality has two different forms based on the values of the positive number 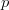 :
:
- If
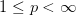 , then
, then 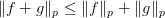 ;
; - If
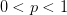 , then
, then 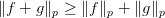 .
.
We provide a one-form Minkowski's inequality for all 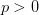 . A non-conjugate Hölder's inequality is also introduced. Some applications of the one-form Minkowski's inequality and non-conjugate Hölder's inequality are introduced too.
. A non-conjugate Hölder's inequality is also introduced. Some applications of the one-form Minkowski's inequality and non-conjugate Hölder's inequality are introduced too.
Wykład odbędzie się w języku angielskim
2015-05-19 Seminarium nieliniowe
Patryk Kołacki
Sterowanie ślizgowe w układach automatyki
(Kontynuacja seminarium z 2015-05-12)
2015-05-12 Seminarium nieliniowe
Patryk Kołacki
Sterowanie ślizgowe w układach automatyki
Seminarium na celu zaprezentowanie jednego z najpopularniejszych rodzajów sterowania nieliniowego, tj. sterowania ślizgowego. Omówione zostanie samo prawo sterowania, jak również jego zastosowania. Całość zilustrowana będzie przykładami obrazującymi ideę tego rodzaju sterowania.
2015-05-05 Seminarium nieliniowe
Adam Nawrocki
Funkcje dwuokresowe
(Kontynuacja seminarium z 2015-04-28)
2015-04-28 Seminarium nieliniowe
Adam Nawrocki
Funkcje dwuokresowe
W referacie omówimy pojęcie funkcji dwuokresowej i funkcji prawie okresowej w kontekście funkcji eliptycznych.
2015-04-21 Seminarium nieliniowe
dr Przemysław Chełminiak
Co łączy komórkę biologiczną z ułamkowym równaniem dyfuzji?
Obserwacja pojedynczych cząsteczek w żywych komórkach biologicznych stała się obecnie możliwa dzięki zastosowaniu nowej techniki obrazowania zwanej spektroskopią pojedynczej molekuły. Co ciekawe, dyfuzja nanocząsteczek, takich jak białka, kwasy nukleinowe, czy też półgiętkie włókna polimerowe w obrębie zatłoczonego wnętrza komórki biologicznej jest wolniejsza od zwyczajnej dyfuzji brownowskiej cząsteczek o rozmiarach mikrometrów zawieszonych w środowisku wodnym. Miarą ich rozprzestrzeniania się wewnątrz komórki jest uśredniony po czasie lub zespole statystycznym cząsteczek kwadrat przebytej odległości, który w tym przypadku nie wzrasta liniowo z czasem. Ponadto, obie procedury uśredniania różnią się od siebie, kiedy czas obserwacji pojedynczej cząsteczki staje się o wiele dłuższy od charakterystycznej skali czasowej samego procesu dyfuzji. W związku z tym przypadkowy ruch cząsteczek w komórce nie może być postrzegany jako zwykły ruchu Browna, lecz musi być rozważany w kategoriach dyfuzji anomalnej (subdyfuzji). Z formalnego punktu widzenia proces ten może być opisany w ramach szeroko stosowanego modelu błądzenia przypadkowego z ciągłym czasem. Zastosujemy tą metodę w celu wyprowadzenia ułamkowego równania Fokkera-Plancka będącego odpowiednikiem równania dyfuzji anomalnej w potencjale sił zewnętrznych blisko równowagi termicznej. Wykorzystując znane metody rachunku różniczkowego pochodnych ułamkowych znajdziemy kilka szczególnych rozwiązań tego równania różniczkowego cząstkowego i pokażemy, że średniokwadratowa odległość przebyta przez anomalnie dyfundujące cząsteczki skaluje się z czasem według prawa potęgowego.
2015-04-14 Seminarium nieliniowe
dr Giselle Monteiro
Nowe twierdzenie o zbieżności abstrakcyjnych całek Kurzweila-Stieltjesa
W teorii całek Riemmanna wpływ twierdzenia Arzeli o zbieżności ograniczonej, zwanego również twierdzeniem Arzeli-Osgooda lub twierdzeniem Osgooda jest porównywalny z wpływem twierdzenia o zbieżności zmajoryzowanej w teorii całek Lebesgue'a. W trakcie seminarium rozważymy abstrakcyjną całkę Kurzweila-Stieltjesa, czyli całkę typu Stieltjesa dla funkcji o wartościach w przestrzeniach Banacha wprowadzoną przez S. Schwabika. Naszym celem będzie przedstawienie twierdzenia o zbieżności ograniczonej w tym przypadku.
2015-03-31 Seminarium nieliniowe
Piotr Maćkowiak
Pewien lemat kombinatoryczny i jego konsekwencje
(Kontynuacja seminarium z 2015-03-17)
2015-03-24 Seminarium nieliniowe
Marcin Borkowski
O pewnym uogólnieniu przestrzeni metrycznej
(Kontynuacja seminarium z 2015-03-10)
2015-03-17 Seminarium nieliniowe
Piotr Maćkowiak
Pewien lemat kombinatoryczny i jego konsekwencje
Na seminarium przedstawimy lemat kombinatoryczny stanowiący o istnieniu dla pewnych triangulacji sympleksu 202424.png) -wymiarowego i przy pewnym etykietowaniu numerami
-wymiarowego i przy pewnym etykietowaniu numerami 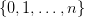 wierzchołków tych triangulacji, takiego łańcucha sympleksów łączącego ’wierzchołek’ z ’podstawą’, że dla każdego sympleksu z tego łańcucha każdy element zbioru
wierzchołków tych triangulacji, takiego łańcucha sympleksów łączącego ’wierzchołek’ z ’podstawą’, że dla każdego sympleksu z tego łańcucha każdy element zbioru 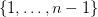 jest etykietą pewnego wierzchołka tego sympleksu. Pokażamy, że (prostymi) konsekwencjami tego lematu są
jest etykietą pewnego wierzchołka tego sympleksu. Pokażamy, że (prostymi) konsekwencjami tego lematu są
- istnienie zer wielowartościowego odwzorowania popytu nadwyżkowego;
- istnienie continuum zer parametryzowanego wielowartościowego odwzorowania popytu nadwyżkowego;
- słynny Lemat Spernera.
2015-03-10 Seminarium nieliniowe
Marcin Borkowski
O pewnym uogólnieniu przestrzeni metrycznej
W czasie referatu podamy aksjomatykę pojęcia 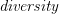 , które uogólnia pojęcie metryki, przedstawimy przykłady
, które uogólnia pojęcie metryki, przedstawimy przykłady 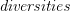 oraz udowodnimy pewne własności tego pojęcia.
oraz udowodnimy pewne własności tego pojęcia.
2015-03-03 Seminarium nieliniowe
Jędrzej Sadowski
Quasikryształy i wzorce prawie okresowe
(Kontynuacja seminarium z 2015-01-20 i 2015-01-27)
2015-02-24 Seminarium nieliniowe
dr Jacek Gulgowski
Zwartość w przestrzeniach funkcji o ograniczonej wariacji
Badanie istnienia punktów stałych odwzorowań w przestrzeni
Banacha często odwołuje się do metod związanych z twierdzeniem Schaudera o punkcie stałym lub do metod stopnia Leray-Schaudera. Obydwa podejścia wymagają pracy z odwzorowaniami pełnociągłymi - warto więc starać zrozumieć wzajemne relacje pomiędzy różnymi przestrzeniami w klasie przestrzeni 202424.png) czy
czy 202424.png) . W szczególności przyjrzymy się pewnym związkom pomiędzy przestrzeniami, które prowadzą do twierdzeń o zwartym włożeniu. Przeanalizujemy również pełnociągłość pewnych operatorów całkowych działających pomiędzy przestrzeniami
. W szczególności przyjrzymy się pewnym związkom pomiędzy przestrzeniami, które prowadzą do twierdzeń o zwartym włożeniu. Przeanalizujemy również pełnociągłość pewnych operatorów całkowych działających pomiędzy przestrzeniami 202424.png) .
.
2015-01-27 Seminarium nieliniowe
Jędrzej Sadowski
Quasikryształy i wzorce prawie okresowe
(Kontynuacja seminarium z 2015-01-20)
2015-01-20 Seminarium nieliniowe
Jędrzej Sadowski
Quasikryształy i wzorce prawie okresowe
(Kontynuacja seminarium z 2015-01-13)
2015-01-13 Seminarium nieliniowe
Jędrzej Sadowski
Quasikryształy i prawie okresowe wzorce
W trakcie seminarium przedstawimy definicję prawie okresowych wzorców (almost periodic patterns), ich podstawowe własności oraz powiązania z quasikryształami.