Marcin Borkowski
Twierdzenia o punktach stałych z warunkiem brzegowym
W 1998 roku Espínola i López udowodnili pewne twierdzenie o punkcie stałym dla odwzorowania działającego z dopuszczalnego podzbioru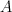 
przestrzeni metrycznej hiperwypukłej w całą tę przestrzeń, przy założeniu, że odwzorowanie to przekształca brzeg zbioru 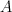w ten zbiór. Pokażemy, jak można znacząco uprościć dowód głównego lematu z ich pracy, zarazem znacząco osłabiając jego założenia. W szczególności, umożliwi to podanie nowego twierdzenia o punkcie stałym, uogólniającego klasyczny wynik Baillona z 1988 roku.