Oto tytuły i streszczenia seminariów z 2010 roku:
2010-12-21 Seminarium nieliniowe
Marcin Borkowski
O formalnych szeregach potęgowych
Celem referatu jest wprowadzenie do teorii formalnych szeregów potęgowych. Po podaniu podstawowych definicji i własności pokażemy przykładowe zastosowania do kombinatoryki. Na koniec pokażemy przykład formalnego rozwiązania równania różniczkowego.
2010-12-14 Seminarium nieliniowe
O kryterium zwartości w przestrzeni funkcji ciągłych i ograniczonych zdefiniowanych na zbiorze niezwartym
2010-12-07 Seminarium nieliniowe
Marcin Wachowiak
Twierdzenie o punktach stałych dla przekształceń spełniających warunek wnętrza
(Kontynuacja seminarium z 2010-11-23 i 2010-11-30).
2010-11-30 Seminarium nieliniowe
Marcin Wachowiak
Twierdzenie o punktach stałych dla przekształceń spełniających warunek wnętrza
(Kontynuacja seminarium z 2010-11-23)
2010-11-23 Seminarium nieliniowe
Marcin Wachowiak
Twierdzenie o punktach stałych dla przekształceń spełniających warunek wnętrza
W referacie pokażemy prawdziwość twierdzenia o punktach
stałych dla przekształceń zgęszczających spełniających nowy warunek typu Leray-Schaudera opracowanego przez Antonio Jimenez-Melado i Claudio H. Moralesa, tzw. warunek wnętrza. Wykażemy i zademonstrujemy na przykładach niezależność tego warunku w ogólnym przypadku od klasycznego warunku brzegowego Leray-Schaudera. Pokażemy również, że dla przestrzeni Hilberta i przekształceń nierozszerzających warunek Leray-Schaudera wynika z warunku wewnętrznego.
2010-11-16 Seminarium nieliniowe
Marcin Borkowski
O pewnych problemach związanych ze splotem funkcji
(Kontynuacja seminariów z 2010-10-26 i 2010-11-09)
2010-11-09 Seminarium nieliniowe
Marcin Borkowski
O pewnych problemach związanych ze splotem funkcji
(Kontynuacja seminarium z 2010-10-26)
2010-10-26 Seminarium nieliniowe
Marcin Borkowski
O pewnych problemach związanych ze splotem funkcji
Splot funkcji całkowalnych w sensie Lebesgue'a jest klasycznym pojęciem, którego przeniesienie na grunt teorii całek nieabsolutnie zbieżnych napotyka na zaskakujące trudności. W referacie przedstawimy niektóre z tych problemów oraz przedstawimy kontrprzykłady pokazujące, że splot zdefiniowany przy użyciu całki Henstocka-Kurzweila nie ma własności analogicznych do przypadku 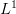 .
.