Zakład Optymalizacji i Sterowania: 2014-05-20 Seminarium nieliniowe

Adam Nawrocki
Asymptotyczne zachowanie pewnej funkcji prawie okresowej wzgledem miary Lebesgue'a

Funkcja

$\begin{displaymath} f(x)=\frac{1}{2+\cos x +\cos{(x\sqrt 2)}} \end{displaymath}$ (1)
jest klasycznym przykładem nieograniczonej i ciągłej funkcji 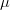$\mu$ -prawie okresowej. Dla tej funkcji zachodzi
$\begin{displaymath} \forall_{\varepsilon>0} \quad \lim_{x\to \infty}\frac{x^{-2-\varepsilon}}{2+\cos x +\cos{(x\sqrt 2)}}=0. \end{displaymath}$ (2)
W referacie omówimy ideę dowodu powyższej równości, w której wykorzystuje się aproksymacje diofantyczne. Pokażemy ponadto, że granica
$\begin{displaymath} \lim_{x\to \infty}\frac{x^{-2}}{2+\cos x +\cos{(x\sqrt 2)}} \end{displaymath}$ (3)
nie istnieje.