Last edit
Changed:
< * [[Seminar|Seminars in 2010]]
to
> * [[Seminar|Seminars in 2011]]
> * [[Seminars in 2010]]
Here are the titles and abstracts of the seminars which were held in 2006:
2006-12-19 Seminar
Ryszard UrbańskiMinimal representations in Minkowski-Radström-Hörmander classes generated by pairs of closed convex and compact sets
Defining suitable topology in the collection of all closed convex subsets of a topological vector space and using ordinal cancellation law and some properties of the cone of compact sets, we obtain representation theorem.
2006-12-12 Seminar
Ryszard Urbański, Jerzy GrzybowskiOn some properties of the Minkowski-Hörmander-Radström lattice
During the lecture, some properties of the Minkowski-Hörmander-Radström lattice will be shown, including Archimedeanness, existence of axial elements, orthogonality.
2006-12-05 Seminar
mgr Danuta Borowska, dr Jerzy GrzybowskiSubtraction and Sallee's elements in semigroups
We can define the Minkowski sum and the Minkowski subtraction in the cone of convex and compact sets. Properties of the the Minkowski subtraction were studied by G.T. Sallee, who formulated the definition of a family of sets, such that the intersection of any collection of translations of the given set is the summand of this set. The Minkowski subtraction was generalized to semigroups by H. Przybycień. During the lecture we will present some properties of the subtraction and we will give the generalization of the notion of a Sallee's set for the semigroups' elements. Moreover, interesting examples of semigroups will be presented.
2006-11-28 Seminar
Marcin BorkowskiOn some Krasnoselskii-type theorem
We present a fixed point theorem for a sum of two multifunctions acting on a weakly compact, hyperconvex subset of a normed space. The theorem is a multivalued version of a result of D. Bugajewski.
2006-11-21 Seminar
Piotr KasprzakFlow invariance over closed sets under general dissipativity conditions
(Continuation of the 2006-11-14 Seminar)
2006-11-14 Seminar
Piotr KasprzakFlow invariance over closed sets under general dissipativity conditions
(Continuation of the 2006-11-07 Seminar)
2006-11-07 Seminar
Piotr KasprzakFlow invariance over closed sets under general dissipativity conditions
During the lecture some flow invariance results will be given for differential equations over Banach spaces under generalized dissipativity conditions. The technical aspect of this approach consist of constructing the approximate solutions and the parwise refinements of these via maximality procedures. The lecture is based on the paper of M. Turinici "Flow invariance over closed sets under general dissipativity conditions", Sci. Ann. Univ. Agric. Sci. Vet. Med. 47 (2004), no. 2, 35--67.
2006-10-27 Seminar
This lecture will be held on Friday on 15.00 in room B3-38
prof. dr hab. Grzegorz Lewicki (Institute of Mathematics of Jagiellonian University)Spaces with maximal projection constant
Let 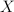 be a real Banach space and
be a real Banach space and 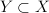 its closed subspace. Denote by
its closed subspace. Denote by 202424.png) the set of all linear and continuous projections from
the set of all linear and continuous projections from 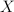 on
on 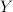 . Let
. Let 3d5cinf5c7b5c7cP5c7c3aP5cin5cmathcal7bP7d(X2cY)5c7d202424.png) . For
. For 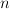 -dimensional Banach space
-dimensional Banach space 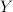 let
let 203d205csup205c7b205clambda(Y2cX)3a20Y205csubset20X205c7d202424.png) . The constant
. The constant 202424.png) is called the absolute projection constant. It is a well-known fact that for
is called the absolute projection constant. It is a well-known fact that for 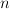 -dimensional Banach space
-dimensional Banach space 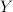 ,
, 203d205clambda(Y2c20l_7b5cinfty7d)202424.png) . For fixed
. For fixed 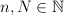 ,
, 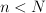 let
let 203d205csup5c7b205clambda(Y)203a20Y205csubset20l_7b5cinfty7d5e7b(N)7d2c5c2c205cdim(Y)203d20n5c7d202424.png) . During the lecture I will present some results and open problems concerning effective determining
. During the lecture I will present some results and open problems concerning effective determining 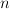 -dimensional spaces
-dimensional spaces 7d202424.png) such that
such that 7d)203d205clambda5eN_n202424.png) .
.
2006-10-24 Seminar
Daria Bugajewska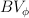 -solutions of nonlinear integral equations
-solutions of nonlinear integral equations
(Continuation of the 2006-10-10 Seminar)
2006-10-17 Seminar
Hubert PrzybycieńSome properties of the Minkowski sum of measurable sets
In this talk we will deal with some properties of the Minkowski sum of measurable sets. We will present the proof of Steinhaus theorem, which states that the Minkowski sum of positive measure sets contains a segment, as well as its application. Moreover we will give an example of a measurable set A, such that the set A+A is non-measurable.
2006-10-10 Seminar
Daria Bugajewska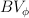 -solutions of nonlinear integral equations
-solutions of nonlinear integral equations
In this talk we will deal with solutions of nonlinear Hammerstein and Volterra-Hammerstein integral equations in the space of functions of bounded 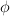 -variation in the sense of Young. We will discuss the existence and in some cases the existence and uniqueness of local and global solutions in this class. Real-valued as well as vector-valued functions will be under our consideration. The method of our proofs is based on an application of the Banach contraction principle as well as the Leray-Schauder alternative for contractions.
-variation in the sense of Young. We will discuss the existence and in some cases the existence and uniqueness of local and global solutions in this class. Real-valued as well as vector-valued functions will be under our consideration. The method of our proofs is based on an application of the Banach contraction principle as well as the Leray-Schauder alternative for contractions.