This lecture will be held on Friday on 15.00 in room B3-38
prof. dr hab. Grzegorz Lewicki (Institute of Mathematics of Jagiellonian University)Spaces with maximal projection constant
Let 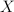 be a real Banach space and
be a real Banach space and 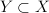 its closed subspace. Denote by
its closed subspace. Denote by 202424.png) the set of all linear and continuous projections from
the set of all linear and continuous projections from 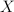 on
on 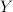 . Let
. Let 3d5cinf5c7b5c7cP5c7c3aP5cin5cmathcal7bP7d(X2cY)5c7d202424.png) . For
. For 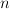 -dimensional Banach space
-dimensional Banach space 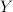 let
let 203d205csup205c7b205clambda(Y2cX)3a20Y205csubset20X205c7d202424.png) . The constant
. The constant 202424.png) is called the absolute projection constant. It is a well-known fact that for
is called the absolute projection constant. It is a well-known fact that for 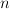 -dimensional Banach space
-dimensional Banach space 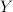 ,
, 203d205clambda(Y2c20l_7b5cinfty7d)202424.png) . For fixed
. For fixed 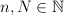 ,
, 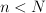 let
let 203d205csup5c7b205clambda(Y)203a20Y205csubset20l_7b5cinfty7d5e7b(N)7d2c5c2c205cdim(Y)203d20n5c7d202424.png) . During the lecture I will present some results and open problems concerning effective determining
. During the lecture I will present some results and open problems concerning effective determining 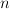 -dimensional spaces
-dimensional spaces 7d202424.png) such that
such that 7d)203d205clambda5eN_n202424.png) .
.