Here are the titles and abstracts of the seminars which were held in 2008:
2008-12-16 Seminar
mgr Paweł Suplicki
Convex Programming
In the talk we will discuss convex programming. Furthermore, we will present symplex algorithm introduced by G.B. Dantzig.
2008-12-09 Seminar
prof. dr hab. Tadeusz Rzeżuchowski (The Faculty of Mathematics and Information Science at the Warsaw University of Technology)
Demyanov metric in the family of convex bounded sets
The seminar will be held at 9.00 in A1-33.
Let  be a linear and continuous functional
be a linear and continuous functional  and
and 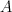 a convex bounded subset of a linear space
a convex bounded subset of a linear space 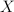 . We call the set
. We call the set 3d5csup_7by5cin20A7df(y)5c7d202424.png) the face of
the face of 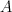 supported by the function
supported by the function  and denote it by
and denote it by 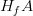 . If
. If 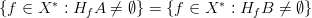 , we define the Demyanov distance between the sets
, we define the Demyanov distance between the sets 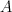 and
and 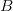 as
as 202424.png) , where
, where 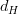 is the usual Hausdorff metric.
is the usual Hausdorff metric.
2008-11-25 Seminar
Paweł Suplicki
Linear Programming
In the talk we will discuss linear and convex programming. Moreover, we will give some examples as well as applications.
2008-11-18 Seminar
mgr Danuta Borowska
On some representations of linear functionals
(Continuation of the 2008-10-28 Seminar)
2008-11-04 Seminar
Ryszard Urbański i Jerzy Grzybowski
Shadowing set and finite exhausters
(Continuation of the 2008-10-07 Seminar and the 2008-10-21 Seminar)
2008-10-28 Seminar
mgr Danuta Borowska
On some representations of linear functionals
2008-10-21 Seminar
Ryszard Urbański and Jerzy GrzybowskiShadowing set and finite exhausters
(Continuation of the 2008-10-07 Seminar)
2008-10-07 Seminar
Ryszard Urbański and Jerzy GrzybowskiShadowing set and finite exhausters
We will introduce the notation of a shadowing set, which is a generalization of the notion of separating set to the family of more than two sets. We will prove some theorems dealing with the shadowing set. Furthermore, we will give the criterion for upper exhauster to be an exhauster of sublinear function as well as the criterion for minimality of finite upper exhauster. All the results will be illustrated by examples.
2008-06-10 Seminar
Mahide Küçük (Anadolu University, Eskişehi, Turcja)
Optimalization over sets defined by inequality constraints
(The lecture will be held at 12.00 in room A1-23)
In the talk, firstly Non Linear Programming problems (NLP) will be presented in 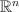 . Then first order necessary condition (Karush-Kuhn-Tucker Theorem), second order necessary condition and one sufficient condition under inequality constraints for NLP problems will be given. This will be followed by examples about the subject. Finally, two sufficient condition for Constrained Qualification (CQ) of NLP problems will be given.
. Then first order necessary condition (Karush-Kuhn-Tucker Theorem), second order necessary condition and one sufficient condition under inequality constraints for NLP problems will be given. This will be followed by examples about the subject. Finally, two sufficient condition for Constrained Qualification (CQ) of NLP problems will be given.
2008-05-13 Seminar
Since prof. Urbański and dr Grzybowski take part in a conference, the seminar on May 13 is cancelled.
2008-05-06 Seminar
Danuta BorowskaProperties of the Minkowski subtraction of convex sets
(Continuation of the 2008-04-29 Seminar)
2008-04-29 Seminar
Danuta BorowskaProperties of the Minkowski subtraction of convex sets
In the talk we will define the Minkowski sum and subtraction in a semigroup. Furhtermore, we will prove some properties of the Minkowski subtraction, summands and the Sallee's sets in the semigropu 202424.png) . We will also discuss the full classification of strongly monotypic polyhedrons in
. We will also discuss the full classification of strongly monotypic polyhedrons in 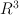 and the relationship between the strongly monotypic polyhedrons and the Sallee's sets.
and the relationship between the strongly monotypic polyhedrons and the Sallee's sets.
2008-04-22 Seminar
Hubert PrzybycieńOn a topological direct sum decomposition of a topological group 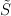
(Continuation of the 2008-04-15 Seminar)
2008-04-15 Seminar
Hubert PrzybycieńOn a topological direct sum decomposition of a topological group 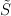
(Continuation of the 2008-04-08 Seminar)
2008-04-08 Seminar
Hubert PrzybycieńOn a topological direct sum decomposition of a topological group 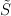
We will prove a topological direct sum decomposition theorem of a topological group 202424.png) into its two subgroups: symmetric and asymetric one, under some assumptions about uniformly continuity of + and so-called symetry operator. Furthermore, we will give some examples.
into its two subgroups: symmetric and asymetric one, under some assumptions about uniformly continuity of + and so-called symetry operator. Furthermore, we will give some examples.
2008-04-01 Seminar
Hubert PrzybycieńOn a direct sum decomposition of a group 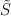
Given a commutative semigroup with the neutral element and the cancellation law 202424.png) , denote by
, denote by 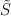 the set
the set 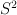 with the equivalence relation
with the equivalence relation 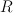 such that
such that R(c2cd)202424.png) if and only if
if and only if 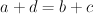 . We will show that
. We will show that 202424.png) is a group and under some assumptions it is possible to decompose
is a group and under some assumptions it is possible to decompose 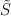 into a direct sum of two subgroups: symmetric and asymmetric one.
into a direct sum of two subgroups: symmetric and asymmetric one.
2008-03-18 Seminar
Danuta BorowskaOn decomposition of closed, convex set theorems.
(Continuation of the 2008-03-11 Seminar)
2008-03-11 Seminar
Danuta BorowskaOn decomposition of closed, convex set theorems.
We will present Klee-Minkowski-Hirsch theorem, which states that every closed, convex set 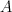 can be decomposed into linearity space
can be decomposed into linearity space 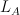 , asymptotic cone
, asymptotic cone 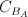 and convex hull of extremal points of the intersection of
and convex hull of extremal points of the intersection of 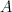 and the orthogonal complement of the linearity space. We will also prove that the above theorem is a generalization of well-known results.
and the orthogonal complement of the linearity space. We will also prove that the above theorem is a generalization of well-known results.
2008-03-04 Seminar
Piotr KasprzakOrthogonality in Birkhoff sense and semi-inner products in Banach spaces
(Continuation of the 2008-02-26 Seminar)
2008-02-26 Seminar
Piotr KasprzakOrthogonality in Birkhoff sense and semi-inner products in Banach spaces
We will introduce the notion of the orthogonality in Birkhoff sense and semi-inner products in Banach spaces. Furthermore, we will present some of their properties and give some examples.
2008-02-19 Seminar
Marcin Borkowski will continue his 22th January talk On orthogonality in normed spaces.
2008-01-22 Seminar
Marcin BorkowskiOn orthogonality in normed spaces
We will discuss two ways of defining orthogonality in spaces without an inner product. The talk will be based on the classical paper by R. C. James.
2008-01-10 Seminar
prof. dr hab. Andrzej Cegielski (Faculty of Mathematics, Computer Science and Econometrics, University of Zielona Góra)
Regular nonexpansive mappings and their applications
2008-01-08 Seminar
Marcin BorkowskiOn some Krasnoselskii type theorems
(Continuation of the 2007-12-04 Seminar)