Here are the titles and abstracts of the seminars which were held in 2007:

2007-12-04 Seminar

Marcin Borkowski
On some Krasnoselskii type theorems

We will prove two fixed point theorems of Krasnoselskii type.

2007-11-27 Seminar

Danuta Borowska and Jerzy Grzybowski
Intersection property in the class of all closed bounded and convex sets.

(Continuation of the 2007-11-13 Seminar)

2007-11-20 Seminar

P. Kawęcki, B. Kraska, K. Majcherek, M. Zoła (lecturer: B. Kraska)
(John Paul II Catholic University of Lublin)

Guarding a line segment

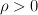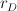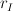A line segment on the plane, equipped with norm $\|(x_{1}, x_{2})\| = \max \{|x_{1}|, |x_{2}|\}$ , is guarded by the defender D. The invader I wants to reach the line segment but he has to keep the distance from the defender no less than a given constant $\rho > 0$ . The defender and the invader can move on the whole plane with maximal speed of $r_{D}$ and $r_{I}$ respectively, where 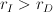$r_{I} > r_{D}$ . No further kinematic or dynamic constrains are imposed on the defender and the invader motions. The maximal length of the line segment which can be guarded by the defender is established in this paper.

2007-11-13 Seminar

Danuta Borowska and Jerzy Grzybowski
Intersection property in the class of all closed bounded and convex sets.

We will discuss the following property of compact convex sets: nonempty intersection of an arbitrary class of translations of a set is a summand (in the Minkowski sense) of the set. We will show that some sets different to polyhedron and ellipsoid, such as wedges, dull wedges and some parts of the Euclidean ball also own the property in question. Moreover, we will prove that the family of all three-dimensional strongly monotypical polyhedrons coincide with the family of all three-dimensional polyhedral sets having the above property.

2007-11-06 Seminar

Marcin Borkowski
Hyperconvex hull revisited

In the talk we will consider hyperconvex spaces with the property that each subset has a unique hyperconvex hull. A necessary and sufficient condition for a space to possess this property will be given.

2007-10-23 Seminar

Hubert Przybycień
On the space of 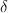$\delta$ -convex functions and its dual

The talk is based on the paper "On the space of 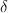$\delta$ -convex functions and its dual" by Urban Cegrell.

2007-10-16 Seminar

Marcin Borkowski
Hyperconvexity and convexity

We will discuss the relation between hyperconvexity and convexity in Banach spaces. We will state the conditions a Banach space must satisfy so that convexity imply hyperconvexity and conversely.

2007-10-09 Seminar

Ryszard Urbański
On minima of families of sublinear functions

In the talk a necessary and sufficient condition for a minimum of finitely many elements of the Minkowski-Rådström-Hörmander space to belong to the cone of nonempty, bounded, closed and convex sets will be given. This result will be applied to show a condition for a minimum of a finite family of support functions to be sublinear.

2007-05-29 Seminar

Ryszard Urbański and Jerzy Grzybowski
Convex and Fractal Geometry conference in Będlewo -- report

2007-05-15 Seminar

Jerzy Grzybowski
On crystal growth

We will present a model of crystal growth and a sufficient and necessary condition for vanishing of facets. We will also compute the derivative and propose a formula for the shape of the crystal at any given moment.

2007-05-08 Seminar

Marcin Borkowski
Darbo type theorems for multifunctions

We will present some Darbo-type theorems for multivalued operators in hyperconvex metric spaces.

(Continuation of the 2007-04-17 Seminar)

2007-04-25 Seminar

This lecture will be held on Wednesday at 12.30

prof. dr hab. Andrzej Fryszkowski (Faculty of Mathematics and Information Science at the Warsaw University of Technology)

Filippov lemma for differential inclusions of higher orders

2007-04-17 Seminar

Marcin Borkowski
Darbo type theorems for multifunctions

We will present some Darbo-type theorems for multivalued operators in hyperconvex metric spaces.

2007-03-28 Seminar

This lecture will be held on Wednesday at 12.30 in room B3-39

prof. dr hab. Tadeusz Rzeżuchowski (The Faculty of Mathematics and Information Science at the Warsaw University of Technology)

On the equivalent differential inclusions and minimal assumptions about convexity of the right side

2007-03-20 Seminar

Hubert Przybycień
On the completeness of the Minkowski-Rådström-Hörmander space

We will consider the problem of completeness of the Minkowski-Rådström-Hörmander space 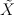$\tilde{X}$ in the case of 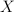$X$ being a metrizable topological vector space.

2007-03-13 Seminar

Ryszard Urbański and Jerzy Grzybowski
Exposed points of the unit ball in the Minkowski-Rådström-Hörmander Space

(Continuation of the 2007-03-06 Seminar)

2007-03-06 Seminar

Ryszard Urbański and Jerzy Grzybowski
Extreme points of the unit ball in the Minkowski-Rådström-Hörmander Space

(Continuation of the 2007-02-27 Seminar)

2007-02-27 Seminar

Ryszard Urbański and Jerzy Grzybowski
Extreme points of the unit ball in the Minkowski-Rådström-Hörmander Space

During the lecture we will prove that the unit ball in the Minkowski-Rådström-Hörmander Space 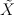$\tilde{X}$ over any normed vector space 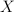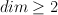$X$ , $dim \geq 2$ , has exactly two extreme points. This result is an effect of the characterization of extreme points of any symmetric interval in the Minkowski-Rådström-Hörmander vector lattice 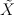$\tilde{X}$ over any Hausdorff topological vector space $X$ .

2007-02-20 Seminar

Hubert Przybycień

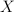2007-01-23 Seminar

Paweł Suplicki
On functions represented as a difference of two convex functions
(Continuation of the 2007-01-16 Seminar)

2007-01-16 Seminar

Paweł Suplicki

On functions represented as a difference of two convex functions