Last edit
Added:
> * [[Seminaria w 2011 roku]]
Oto tytuły i streszczenia seminariów z 2006 roku i starszych:
2006-12-19 Seminarium
Ryszard UrbańskiMinimalne reprezentacje w klasach Minkowskiego-Radströma-Hörmandera generowane przez pary zbiorów domkniętych wypukłych i zwartyych
Wprowadzając odpowiednią topologię w klasie podzbiorów domkniętych wypukłych przestrzeni liniowo-topologicznej, korzystając z porządkowego prawa skreśleń oraz własności stożka zbiorów zwartych, otrzymujemy twierdzenie reprezentacyjne.
2006-12-12 Seminarium
Ryszard Urbański, Jerzy GrzybowskiO pewnych własnościach kraty Minkowskiego-Radströma-Hörmandera
Referat będzie poświęcony zaprezentowaniu pewnych własności kraty Minkowskiego-Radströma-Hörmandera, takich, jak archimedesowość, istnienie elementów osiowych, ortogonalność.
2006-12-05 Seminarium
mgr Danuta Borowska, dr Jerzy GrzybowskiOdejmowanie oraz elementy Sallee'go w semigrupie
W stożku zbiorów zwartych wypukłych mamy określone dodawanie oraz odejmowanie Minkowskiego. Własności odejmowania badane były m.in. przez G.T. Sallee'go, który zdefiniował rodzinę zbiorów takich, że przekrój każdej ilości translacji danego zbioru jest sumantem tego zbioru. Na semigrupę odejmowanie uogólnił H. Przybycień. Podczas referatu podamy własności odejmowania oraz uogólnimy pojęcie zbioru Sallee'go na elementy semigrupy oraz przedstawimy ciekawe przykłady semigrup.
2006-11-28 Seminarium
Marcin BorkowskiO pewnym twierdzeniu typu Krasnosielskiego
Przedstawimy twierdzenie o punkcie stałym dla sumy dwóch multifunkcji działających na słabo zwartym, hiperwypukłym podzbiorze przestrzeni unormowanej. Twierdzenie jest wielowartościowym odpowiednikiem wyniku D. Bugajewskiego.
2006-11-21 Seminarium
Piotr KasprzakO pewnych zagadnieniach z teorii równań różniczkowych w przestrzeniach Banacha
(Kontynuacja seminarium z 2006-11-14)
2006-11-14 Seminarium
Piotr KasprzakO pewnych zagadnieniach z teorii równań różniczkowych w przestrzeniach Banacha
(Kontynuacja seminarium z 2006-11-07)
2006-11-07 Seminarium
Piotr KasprzakO pewnych zagadnieniach z teorii równań różniczkowych w przestrzeniach Banacha
Referat poświęcony będzie rezultatom dotyczącym niezmienniczości przepływu dla równań różniczkowych w przestrzeniach Banacha z pewnymi warunkami dyssypatywności. Zastosowane techniki obejmują konstruowanie rozwiązań przybliżonych oraz argumenty typu maksymalności. Referat oparty jest na pracy M. Turiniciego "Flow invariance over closed sets under general dissipativity conditions", Sci. Ann. Univ. Agric. Sci. Vet. Med. 47 (2004), no. 2, 35--67.
2006-10-27 Seminarium
Wykład odbędzie się w piątek o 15.00 w sali B3-38
prof. dr hab. Grzegorz Lewicki (Instytut Matematyki Uniwersytetu Jagiellońskiego)
Przestrzenie z maksymalną stałą projekcji
Niech 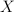 będzie przestrzenią Banacha nad
będzie przestrzenią Banacha nad 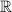 , a
, a 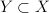 jej podprzestrzenią domkniętą. Oznaczmy symbolem
jej podprzestrzenią domkniętą. Oznaczmy symbolem 202424.png) wszystkie rzutowania liniowe i ciągłe z
wszystkie rzutowania liniowe i ciągłe z 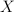 na
na 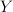 . Niech
. Niech 3d5cinf5c7b5c7cP5c7c3aP5cin5cmathcal7bP7d(X2cY)5c7d202424.png) . Dla
. Dla 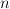 -wymiarowej przestrzeni Banacha
-wymiarowej przestrzeni Banacha 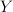 niech
niech 203d205csup205c7b205clambda(Y2cX)3a20Y205csubset20X205c7d202424.png) . Stała
. Stała 202424.png) nazywana jest w literaturze absolutną stałą projekcji. Jest znanym faktem, że dla
nazywana jest w literaturze absolutną stałą projekcji. Jest znanym faktem, że dla 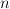 -wymiarowej przestrzeni Banacha
-wymiarowej przestrzeni Banacha 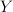 ,
, 203d205clambda(Y2c20l_7b5cinfty7d)202424.png) . Dla ustalonych
. Dla ustalonych 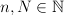 ,
, 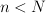 niech
niech 203d205csup5c7b205clambda(Y)203a20Y205csubset20l_7b5cinfty7d5e7b(N)7d2c5c2c205cdim(Y)203d20n5c7d202424.png) . Podczas referatu przedstawię kilka rezultatów i otwartych problemów związanych z efektywnym wyznaczaniem
. Podczas referatu przedstawię kilka rezultatów i otwartych problemów związanych z efektywnym wyznaczaniem 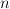 -wymiarowych przestrzeni
-wymiarowych przestrzeni 7d202424.png) takich, że
takich, że 7d)203d205clambda5eN_n202424.png) .
.
2006-10-24 Seminarium
Daria Bugajewska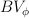 -rozwiązania nieliniowych równań całkowych
-rozwiązania nieliniowych równań całkowych
(Kontynuacja seminarium z 2006-10-10)
2006-10-17 Seminarium
Hubert PrzybycieńPewne własności sumy Minkowskiego zbiorów mierzalnych
Zajmiemy się pewnymi własnościami sumy Minkowskiego zbiorów mierzalnych; m.in. podamy dowód Twierdzenia Steinhausa, mówiącego, że suma Minkowsiego zbiorów o mierze dodatniej zawiera odcinek, oraz zastosowanie tego twierdzenia. Przedstawimy również przykład zbioru mierzalnego A takiego, że zbiór A+A jest niemierzalny.
2006-10-10 Seminarium
Daria Bugajewska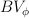 -rozwiązania nieliniowych równań całkowych
-rozwiązania nieliniowych równań całkowych
Referat poświęcony będzie rozwiązaniom nieliniowych równań całkowych Hammersteina i Volterry--Hammersteina w przestrzeni funkcji o ograniczonej 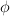 -wariacji w sensie Younga. Przedyskutujemy istnienie, a pewnych przypadkach również jedyność lokalnych i globalnych rozwiązań w tej klasie. Będziemy rozważać zarówno funkcje o wartościach rzeczywistych, jak i wektorowych. Metoda dowodowa jest oparta na zastosowaniu twierdzenia Banacha o kontrakcji oraz alternatywy Leraya--Schaudera dla kontrakcji.
-wariacji w sensie Younga. Przedyskutujemy istnienie, a pewnych przypadkach również jedyność lokalnych i globalnych rozwiązań w tej klasie. Będziemy rozważać zarówno funkcje o wartościach rzeczywistych, jak i wektorowych. Metoda dowodowa jest oparta na zastosowaniu twierdzenia Banacha o kontrakcji oraz alternatywy Leraya--Schaudera dla kontrakcji.
2006-04-01 Wykład im. Ambrożego Kleksa
II Uroczysty Wykład im. prof. Ambrożego Kleksa
Prof. Christopher F. Robin (Uniwersytet Lasu Stumilowego)O teorii Hohoni
Celem wykładu jest zaprezentowanie Ostatnich Wyników
w Bardzo Ważnej I Żywo Się Rozwijającej GałęziMatematyki, jaka z pewnością jest teoria Hohoni. Punktem wyjścia naszych rozważań będzie nietrywialna obserwacja, ze dla każdego Misia istnieje Stworzonko O Jeszcze Mniejszym Rozumku. Zobaczymy, jak wraz z Twierdzeniem O Pułapce fakt ten pozwala uzyskać głęboki wynik egzystencjalny o istnieniu Hohonia (ponieważ w dowodzie w istotny sposób interweniuje Lemat Kłapouchego-Sowy, nie powinno zaskakiwać, ze nikt nigdy żadnego Hohonia nie widział). Dowody prowadzone będą w oparciu o interesującą technikę (odkrytą niezależnie przez Kubusia Puchatka oraz rzesze anonimowych wykładowców) zwaną Dowodzeniem Przez Mruczenie.
2005-04-01 Wykład im. Ambrożego Kleksa
I Uroczysty Wykład im. prof. Ambrożego Kleksa
Prof. Ł. Klides (Aleksandria)O nowym ujęciu geometrii
Wykład poświęcony jest zastosowaniu w geometrii tzw. metody aksjomatycznej, zaproponowanej ostatnio przez pp. Platona i Arystotelesa. Pokażemy, jak w duchu tej nowej, obiecującej metody można zrekonstruować całość znanej obecnie geometrii - od twierdzeń stosowanych już przez starożytnych Egipcjan aż do niedawnych, głębokich rezultatów p. Eudoksosa dotyczących mierzenia figur. Jako przykład podamy piękny dowód nowego wyniku stwierdzającego, że jest więcej liczb pierwszych niż w dowolnym ich zbiorze. Referat oparty jest na przygotowywanej właśnie do publikacji monografii Elementy, która zawierać będzie również pełne dowody prezentowanych twierdzeń.
2004-04-01 Wykład prof. Ambrożego Kleksa
Wykład wydziałowy
prof. Ambroży Kleks (Uniwersytet w Salamance)O abstrakcyjnej teorii piegów
W czasie wykładu omówione zostanie zarówno tradycyjne ujęcie teorii piegów, jak i ujęcie abstrakcyjne, wyrosłe na styku nowoczesnej analizy kleksalnej i algebry kleksologicznej. Dowody będą prowadzone przy wykorzystaniu pewnych głębokich własności CW-kleksów. Pokażemy też zastosowanie do teorii operatorów Bąbla w przestrzeniach lokalnie piegowatych.