Oto tytuły i streszczenia seminariów z 2010 roku:
2010-12-21 Seminarium
Piotr Kasprzak
Zastosowanie stożka 202424.png)
w teorii multifunkcji
Podczas referatu przedstawimy m.in. pewne twierdzenia o przedłużaniu dla multifunkcji. Kluczową rolę w dowodach omawianych wyników odgrywać będzie zastosowanie twierdzenia o zanurzeniu stożka niepustych, domkniętych, ograniczonych oraz wypukłych podzbiorów przestrzeni unormowanej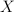 
w pewną przestrzeń Banacha. Referat będzie oparty na pracy Anny Kuci Applications of the Radström-Hörmander Embedding Theorem to Multifunctions, Bull. Acad. Pol. Sci. Math. 53 (3) (2005), 259-271.
2010-12-07 Seminarium
Pewne własności stożka MRH
Podczas referatu podamy warunki konieczne oraz dostateczne, by stożek MRH był kratą. Omówimy również tzw. własność translacji przekroju.
2010-11-30 Seminarium
Seminarium Zakładowe w dniu 2010-11-30 zostało odowłane.
2010-11-23 Seminarium
Jerzy Grzybowski
O podzbiorach ekstremalnych
(Kontynuacja seminarium z 2010-10-26 i 2010-11-09).
2010-11-09 Seminarium
Jerzy Grzybowski
O podzbiorach ekstremalnych
(Kontynuacja seminarium z 2010-10-26).
2010-10-26 Seminarium
Jerzy Grzybowski
O podzbiorach ekstremalnych
W referacie podamy wzór na podzbiór ekstremalny zbioru oraz pokażemy jego zastosowanie do badania jedyności odcinków metrycznych w stożku zbiorów wypukłych z metryką Hausdorffa.
2010-10-19 Seminarium
Daria Bugajewska
O operatorze superpozycji w przestrzeni funkcji o ograniczonej wariacji wraz z zastosowaniami do nieliniowych równań całkowych
(Kontynuacja seminarium z 2010-10-05 i 2010-10-12.)
2010-10-12 Seminarium
Daria Bugajewska
O operatorze superpozycji w przestrzeni funkcji o ograniczonej wariacji wraz z zastosowaniami do nieliniowych równań całkowych
(Kontynuacja seminarium z 2010-10-05.)
2010-10-05 Seminarium
O operatorze superpozycji w przestrzeni funkcji o ograniczonej wariacji wraz z zastosowaniami do nieliniowych równań całkowych
Podczas referatu podamy warunki wystarczające, by operator superpozycji przekształcał przestrzeń funkcji o ograniczonej wariacji w siebie. Będziemy nie tylko rozważać wariacje wsensie Jordana, ale także wariację w sensie Younga oraz tak zwaną uogólnioną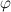 
-wariację. Przestawione wyniki zastosujemy do wykazania twierdzeń o istnieniu i jedyności rozwiązań (lokalnych oraz globalnych) dla nieliniowych równań całkowych Hammersteina czy Volterry-Hammersteina w klasie funkcji o ograniczonej wariacji.
2010-06-22 Seminarium
Xiao-Xiong Gan
(Mathematics Department, Morgan State University, Baltimore, USA)
Just-In-Time Transportation Problem and Its Algorithm
Just-In-Time (JIT) philosophy or management was originally introduced by Toyota Automobiles. JIT management considers that the storage is a waste and hence eliminating storage equals eliminating the waste.
This presentation introduces the JIT-Transportation problem, which requires that all demanded good be shipped to their destination on schedule, at the zero or minimal destination-storage cost. The JIT-Transportation problem is a special goal programming problem with discrete constraints. We provide a mathematical model for such transport problem and introduce the JIT solution, the deviation solution, the JIT deviation, etc. By introducing the 202424.png)
-problem we establish the equivalence between the optimal solution of -problem and the optimal solutions of JIT-Transportation problem, and then provide an algorithm for the JIT-Transportation problems. This algorithm is proven mathematically and is also illustrated by an example.
Wykład odbędzie się w języku angielskim
2010-06-08 Seminarium
Jerzy Grzybowski
Pary minimalne zbiorów ograniczonych, domkniętych oraz wypukłych jako minimalna reprezentacja elementów przestrzeni Minkowskiego-Rådströma-Hörmandera
Teoria par minimalnych zbiorów ograniczonych, domkniętych oraz wypukłych została szczegółowo omówiona w monografii D. Pallaschke and R. Urbańskiego pt. Pairs of Compact Convex Sets, Fractional Arithmetic with Convex Sets. Podczas seminarium omówimy najważniejsze wyniki tej teorii, jak również zaprezentujemy ciekawe przykłady.
2010-05-25 Seminarium
Ryszard Urbański
Zacienianie zbiorów i zastosowanie do rodzin wyczerpujących
Podczas referatu zdefiniujemy oraz podamy pewne własności
zacieniania zbiorów. Zaprezentujemy także zastosowanie zacieniania zbiorów do wykazania kryterium minimalności rodzin wyczerpujących.
2010-05-11 Seminarium
Didem Tozkan
Instytut Matematyki, Wydział Nauk Przyrodniczych, Anadolu University, Eskişehir, Turcja
Pary minimalne zwartych oraz wypukłych podzbiorów przestrzeni topologicznych
Podczas referatu wykażemy pewne własności par minimalnych zwartych oraz wypukłych podzbiorów przestrzeni topologicznej. Podamy również warunki geometryczne, aby para zbiorów wypukłych, zwartych była parą minimalną.
2010-04-27 Seminarium
Ryszard Urbański
Różnica Minkowskiego w półgrupie
2010-04-20 Seminarium
Jerzy Grzybowski
O zanurzeniu stożka zbiorów wypukłych w stożek MRH
(Kontynuacja seminariów z 2010-04-13, 2010-03-23 i 2010-03-16.)
2010-04-13 Seminarium
Jerzy Grzybowski
O zanurzeniu stożka zbiorów wypukłych w stożek MRH
(Kontynuacja seminariów z 2010-03-16 i 2010-03-23.)
2010-03-23 Seminarium
Ryszard Urbański
O zanurzeniu stożka zbiorów wypukłych w stożek MRH
(Kontynuacja seminarium z 2010-03-16)
2010-03-16 Seminarium
Ryszard Urbański
O zanurzeniu stożka zbiorów wypukłych w stożek MRH
(Kontynuacja seminarium z 2010-03-09)
2010-03-09 Seminarium
Ryszard Urbański
O zanurzeniu stożka zbiorów wypukłych w stożek MRH
Podczas referatu wykażemy istnienie zanurzenia stożka 202424.png)
, którego elementami są niepuste, domknięte oraz wypukłe podzbiory rzeczywistej przestrzeni liniowo-topologicznej Hausdorffa, w uogólniony stożek MRH.
2010-03-02 Seminarium
dr Wojciech Kowalewski (Zakład Teorii Przestrzeni Funkcyjnych)
O równaniach Naviera-Stokesa
(Kontynuacja seminarium z 2010-02-16)
2010-02-16 Seminarium
dr Wojciech Kowalewski (Zakład Teorii Przestrzeni Funkcyjnych)
O równaniach Naviera-Stokesa
Na początek przedstawimy zarys teorii numerycznego rozwiązywania równań różniczkowych. W drugiej części wyprowadzimy równania Naviera-Stokesa oraz omówimy problemy związane z ich numerycznym rozwiązywaniem.
2010-01-05 Seminarium
Paweł Suplicki
Algorytm obliczania różnicy Minkowskiego zbiorów
Podczas seminarium omówimy algorytm obliczania różnicy Minkowskiego zbiorów (niekoniecznie wypukłych) autorstwa Světlany Tomiczkovej z University of West Bohemia.