Oto tytuły i streszczenia seminariów z 2012 roku:

2012-12-18 Seminarium nieliniowe

Monika Naskręcka
Homeomorfizm pomiędzy przestrzenią wielomianów i przestrzenią ich pierwiastków

(Kontynuacja Seminarium z dnia 2012-12-11)

2012-12-11 Seminarium nieliniowe

Monika Naskręcka
Homeomorfizm pomiędzy przestrzenią wielomianów i przestrzenią ich pierwiastków

W trakcie seminarium zostanie przedstawiony elementarny, topologiczny dowód twierdzenia o ciągłości pierwiastków zespolonych wielomianu względem jego współczynników. Dla wielomianów unormowanych o współczynnikach zespolonych i dla odpowiednio zdefiniowanych przestrzeni metrycznych twierdzenie to może być wyrażone jako homeomorfizm pomiędzy odpowiadającymi sobie przestrzeniami metrycznymi wielomianów i ich pierwiastków.

2012-12-04 Seminarium nieliniowe

Piotr Maćkowiak
Istnienie zer funkcji popytu nadwyżkowego

(Kontynuacja Seminarium z 2012-10-09 i 2012-10-16.)

2012-11-27 Seminarium nieliniowe

Piotr Zdanowicz
Podstawowe własności szeregów formalnych

(Kontynuacja Seminarium z 2012-11-20)

2012-11-20 Seminarium nieliniowe

Piotr Zdanowicz
Podstawowe własności szeregów formalnych

2012-11-13 Seminarium nieliniowe

Piotr Kasprzak
O pewnej klasie funkcji o 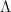$\Lambda$ -ograniczonej wariacji

(Kontynuacja Seminarium z 2012-10-30)

2012-11-06 Seminarium nieliniowe

Seminarium odbędzie się o godzinie 8:30 w Sali Posiedzeń Rady Wydziału (A1-33/34)

Justyna Signerska
Analiza modelu neuronu z prawie okresową funkcją wejścia.

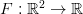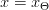Rozważmy układ typu integrate-and-fire $\dot{x}=F(t,x)$ , $F:\mathbb{R}^2\to \mathbb{R}$ , w którym ciągła dynamika jest zaburzona w następujący sposób: $\lim_{t\to s^+}x(t)=x_r$ jeśli $x(s)=x_{\Theta}$ , tj. jeśli zmienna dynamiczna $x(t)$ osiąga pewną ustaloną wartość progową $x=x_{\Theta}$ , jest natychmiast ,,resetowana do wartości spoczynkowej 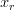$x_r$ i układ ewoluuje od nowa zgodnie z równaniem różniczkowym itd. Pytanie: W jaki sposób opisać szereg czasowy kolejnych resetowań (ang. 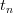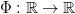spikes) $t_n$ jako kolejne iteracje $\Phi^n(t_0)$ pewnego odwzorowania $\Phi:\mathbb{R}\to \mathbb{R}$ , zwanego firing map, a ciąg interspike-intervals/ 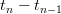$t_n-t_{n-1}$ jako ciąg przemieszczeń $\Phi^n(t_0)-\Phi^{n-1}(t_0)$ wzdłuż trajektorii tego odwzorowania? Problem ten pojawia się m.in. w modelowaniu aktywności komórek nerwowych.

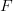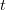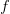Jednakże dotychczas właściwości firing map były badane analitycznie jedynie przy założeniu, że funkcja $F$ jest dostatecznie gładka i często także okresowa względem zmiennej $t$ . My prezentujemy pełny opis własności firing map dla najpopularniejszych modeli $\dot{x}=-\sigma x+f(t)$ (tzw. Leaky Integrate-and-Fire) oraz $\dot{x}=f(t)$ (tzw. Perfect Integrator), gdzie funkcja $f$ jest jedynie lokalnie całkowalna i/lub prawie okresowa. W szczególności okazuje się, że 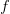$f$ prawie okresowa w sensie Stepanova daje firing map 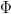$\Phi$ z przemieszczeniem 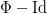$\Phi-\textrm{Id}$ prawie okresowym w sensie Bohra, co stanowi wstęp do formalnej analizy ciągu interspike-intervals w przypadku prawie okresowym.

2012-10-30 Seminarium nieliniowe

Piotr Kasprzak
O pewnej klasie funkcji o 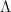$\Lambda$ -ograniczonej wariacji

Podczas seminarium zdefiniujemy szczególną klasę funkcji o 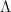$\Lambda$ -ograniczonej wariacji, jak również wykażemy pewne własności takich funkcji. Zajmiemy się także badaniem wspomnianej klasy jako takiej; w szczególności udowodnimy, iż przy odpowiednim wyborze normy klasa ta staje się ściśle wypukłą przestrzenią Banacha. Nasze rozważania zilustrowane będą szeregiem nietrywialnych przykładów.

2012-10-23 Seminarium nieliniowe

Piotr Kasprzak
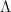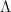O pewnej klasie funkcji o $\Lambda$ -ograniczonej wariacji

2012-10-16 Seminarium nieliniowe

Piotr Maćkowiak
Istnienie zer funkcji popytu nadwyżkowego

(Kontynuacja Seminarium z 2012-10-09)

2012-10-09 Seminarium nieliniowe

Piotr Maćkowiak
Istnienie zer funkcji popytu nadwyżkowego

W trakcie seminarium zostanie przedstawiony dowód istnienia zer dla dowolnej ciągłej funkcji określonej na otwartym sympleksie standardowym o wartościach w przestrzeni, w której ten sympleks jest zawarty i spełniającej: 1) prawo Walrasa; 2) pewien ('prawie' typowy) warunek zachowania blisko brzegu dziedziny; 3) ograniczonej z dołu. Dowód przebiega w dwóch etapach: w pierwszym udowadnia się pewien lemat kombinatoryczny (swoisty odpowiednik lematu Spernera) dla triangulacji Kuhna, a w drugim stosujemy ten lemat do odpowiednio skonstruowanej funkcji o dziedzinie identycznej z dziedziną funkcji popytu nadwyżkowego, ale o wartościach w przestrzeni o zmnijeszonym wymiarze. Dowód zawiera algorytm aproksymacji zer (właściwie: wartości zerowych) z dowolną, ale zadaną z góry dokładnością.

2012-10-02 Seminarium nieliniowe

Seminarium Organizacyjne

2012-05-29 Seminarium nieliniowe

Piotr Kasprzak
O pewnej klasie funkcji o ograniczonej wariacji

(Kontynuacja seminarium z 2012-04-24)

2012-05-22 Seminarium nieliniowe

Michał Burzyński
Alternatywne dowody Twierdzenia Arrowa o Niemożliwości
(Kontynuacja seminarium z 2012-05-08)

2012-05-15 Seminarium nieliniowe

Michał Burzyński
Alternatywne dowody Twierdzenia Arrowa o Niemożliwości.

(Kontynuacja seminarium z 2012-05-08)

2012-05-08 Seminarium nieliniowe

Michał Burzyński
Alternatywne dowody Twierdzenia Arrowa o Niemożliwości.

Twierdzenie Arrowa o Niemożliwości orzeka, iż w przypadku istnienia co najmniej trzech potencjalnych stanów społecznych, nie istnieje taka społeczna funkcja bogactwa 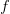$f$ (opisująca preferencje społeczeństwa jako całości przy danych indywidualnych preferencjach), która spełnia cztery warunki: 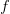$f$ posiada nieograniczoną dziedzinę; silna relacja preferencji społecznych spełnia słabą zasadę Pareto; 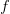$f$ spełnia własność niezależności nieistotnych alternatyw oraz w społeczeństwie o preferencjach opisanych funkcją 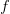$f$ nie występuje dyktator. Oryginalny dowód K. Arrowa składa się z dwóch kroków: pokazania istnienia jednostki decydującej oraz udowodnienia, że musi być ona dyktatorem. Pierwszy z alternatywnych dowodów opiera się na wykorzystaniu preferencji Condorcet. Drugi stosuje krok pierwszy z dowodu Arrowa i wskazuje, że wszystkie decyzje społeczne podejmowane są w identyczny sposób. Ostatni dowód ma charakter graficzny.

2012-04-24 Seminarium nieliniowe

Piotr Kasprzak
O pewnej klasie funkcji o ograniczonej wariacji

Podczas seminarium zdefiniujemy stosunkowo dużą klasę funkcji o ograniczonej wariacji określonych na otwartym podzbiorze 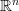$\mathbb R^n$ , która w szczególności zawiera przestrzeń Sobolewa $W^{1,1}(\Omega)$ . Ponadto podamy związki zachodzące pomiędzy uogólnioną wariacją oraz klasyczną wariacją w sensie Jordana.

2012-04-03 Seminarium nieliniowe

Piotr Kasprzak
O kryterium zwartości w przestrzeni funkcji ciągłych i ograniczonych zdefiniowanych na zbiorze niezwartym

Podczas seminarium omówimy pewne kryterium zwartości w przestrzeni funkcji ciągłych i ograniczonych zdefiniowanych na zbiorze niezwartym związane z twierdzeniem Arzeli-Ascolego.

2012-03-27 Seminarium nieliniowe

Piotr Maćkowiak
Twierdzenie o punkcie eksplodującym
Przedstawimy oraz udowodnimy twierdzenie o punkcie eksplodującym autorstwa W.Kulpy. Twierdzenie to stanowi, że dla funkcji określonej na zbiorze zwartym X , zawierającym kostkę K o środku w zerze w swoim wnętrzu, o wartościach w X\K i która jest identycznością na brzegu zbioru X, istnieje taki punkt c w X, że w dowolnym jego otoczeniu znajduje się punkt x taki, że wartości f(x) oraz f(c) są położone po przeciwległych ścianach kostki K.

2012-03-20 Seminarium nieliniowe

Adam Nawrocki
Zastosowanie ułamków łańcuchowych
Podczas seminarium omówimy podstawowe własności ułamków łańcuchowych.
Następnie przejdziemy do zastosowania tych własności przy wyznaczaniu granicy funkcji:
$\lim_{x\rightarrow\infty}\frac{e^{-x}}{2+\cos(x)+\cos(\sqrt{2}x)}$

(Kontynuacja seminarium z 2012-03-13)

2012-03-13 Seminarium nieliniowe

2012-03-06 Seminarium nieliniowe

Marcin Wachowiak
Zastosowania twierdzenia Hopfa-Lefschetza o punkcie stałym
(Kontynuacja seminarium nieliniowego z 2011-11-22, 2011-11-29 oraz 2011-12-06.)

2012-02-28 Seminarium nieliniowe

Jędrzej Sadowski
Definicje funkcji N-prawie okresowych

(Kontynuacja seminarium nieliniowego z 2011-12-20, 2012-01-03, 2012-02-14 i 2012-02-21.)

2012-02-21 Seminarium nieliniowe

Jędrzej Sadowski
Definicje funkcji N-prawie okresowych
(Kontynuacja seminarium nieliniowego z 2011-12-20, 2012-01-03 i 2012-02-14.)

2012-02-14 Seminarium nieliniowe

Jędrzej Sadowski
Definicje funkcji N-prawie okresowych
(Kontynuacja seminarium nieliniowego z 2011-12-20 i 2012-01-03.)

2012-01-24 Seminarium nieliniowe

Daria Bugajewska
O równaniach różniczkowych i całkowych w przestrzeniach o ograniczonej Lambda-wariacji

(Kontynuacja seminarium nieliniowego z 2012-01-10 i 2012-01-17.)

2012-01-17 Seminarium nieliniowe

Daria Bugajewska
O równaniach różniczkowych i całkowych w przestrzeniach o ograniczonej Lambda-wariacji

(Kontynuacja seminarium nieliniowego z 2012-01-10.)

2012-01-10 Seminarium nieliniowe

Daria Bugajewska
O równaniach różniczkowych i całkowych w przestrzeniach o ograniczonej Lambda-wariacji
Rozważane będą liniowe równania różniczkowe oraz nieliniowe równania całkowe w przestrzeniach funkcji o ograniczonej Lambda-wariacji. Podane zostaną twierdzenia o istnieniu oraz o istnieniu i jednoznaczności rozwiązań w tych przestrzeniach oraz w podprzestrzeniach funkcji ciągłych o ograniczonej Lambda-wariacji.

2012-01-03 Seminarium nieliniowe

Jędrzej Sadowski
Definicje funkcji N-prawie okresowych
(Kontynuacja seminarium nieliniowego z 2011-12-20.)