Oto tytuły i streszczenia seminariów z 2008 roku:

2008-12-16 Seminarium

mgr Paweł Suplicki
Programowanie wypukłe

Podczas referatu omówimy programowanie wypukłe, a także szczegółowo zaprezentujemy, wprowadzony przez G.B. Dantziga, algorytm sympleksów.

2008-12-09 Seminarium

prof. dr hab. Tadeusz Rzeżuchowski (Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej)

Metryka Demianowa w rodzinie zbiorów wypukłych i
ograniczonych

Seminarium odbędzie się wyjątkowo o godzinie 9.00 w sali A1-33.

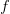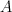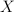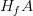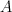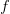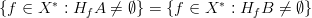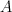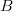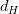Dla funkcji liniowej ciągłej $f$ i podzbioru wypukłego ograniczonego $A$ przestrzeni liniowej $X$ ścianą $H_fA$ zbioru $A$ podpartą przez $f$ nazywamy zbiór $\{x\in A:f(x)=\sup_{y\in A}f(y)\}$ . Jeżeli $\{f\in X^*:H_fA\ne\emptyset\}=\{f\in X^*:H_fB\ne\emptyset\}$ , to odległością Demianowa zbiorów $A$ i $B$ nazywamy $\sup_f d_H(H_fA,H_fB)$ , gdzie $d_H$ jest odległością Hausdorffa zbiorów.

2008-12-02 Seminarium

mgr Paweł Suplicki
Programowanie liniowe

(Kontynuacja seminarium z 2008-11-25)

2008-11-25 Seminarium

mgr Paweł Suplicki
Programowanie liniowe

Podczas referatu omówimy zagadnienia programowania
liniowego oraz wypukłego, a także podamy przykłady, jak
również zastosowania.

2008-11-18 Seminarium

mgr Danuta Borowska
O pewnych reprezentacjach funkcjonałów liniowych

(Kontynuacja seminarium z 2008-10-28)

2008-11-04 Seminarium

Ryszard Urbański i Jerzy Grzybowski
Zbiór zacieniający i skończone exhaustery

(Kontynuacja seminarium z 2008-10-07 i z 2008-10-21)

2008-10-28 Seminarium

mgr Danuta Borowska
O pewnych reprezentacjach funkcjonałów liniowych

2008-10-21 Seminarium

Ryszard Urbański i Jerzy Grzybowski
Shadowing set and finite exhausters

(Kontynuacja seminarium z 2008-10-07)

2008-10-07 Seminarium

Ryszard Urbański i Jerzy Grzybowski
Shadowing set and finite exhausters

We will introduce the notation of a shadowing set, which is a generalization of the notion of separating set to the family of more than two sets. We will prove some theorems dealing with the shadowing set. Furthermore, we will give the criterion for upper exhauster to be an exhauster of sublinear function as well as the criterion for minimality of finite upper exhauster. All the results will be illustrated by examples.

2008-06-10 Seminarium

Mahide Küçük (Anadolu University, Eskişehi, Turcja)

Optimalization over sets defined by inequality constraints

(wykład w ramach programu wymiany pracowników Erasmus; wykład odbędzie się w sali posiedzeń Rady Wydziału o godzinie 12.00)

In the talk, firstly Non Linear Programming problems (NLP) will be presented in 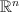$\mathbb{R}^{n}$ . Then first order necessary condition (Karush-Kuhn-Tucker Theorem), second order necessary condition and one sufficient condition under inequality constraints for NLP problems will be given. This will be followed by examples about the subject. Finally, two sufficient condition for Constrained Qualification (CQ) of NLP problems will be given.

2008-05-13 Seminarium

W związku z wyjazdem prof. Urbańskiego i dra Grzybowskiego na konferencję seminarium w dniu 13 maja nie odbędzie się.

2008-05-06 Seminarium

Danuta Borowska

Własności różnicy Minkowskiego zbiorów wypukłych

(Kontynuacja seminarium z 2008-04-29)

2008-04-29 Seminarium

Danuta Borowska

Własności różnicy Minkowskiego zbiorów wypukłych

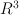W wygłoszonym referacie przedstawiona zostanie rola różnicy Minkowskiego i sumantów w półgrupach. Podane zostaną pewne własności różnicy Minkowskiego, sumantów oraz zbiorów Salle'ego w półgrupie $K(X)$ . Omówiona będzie również pełna klasyfikacja silnie monotypicznych wielościanów w $R^{3}$ oraz zależność między tymi wielościanami a zbiorami Salle'ego.

2008-04-22 Seminarium

Hubert Przybycień

Twierdzenia o rozkładzie grupy topologicznej 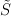$\tilde{S}$ na topologiczną sumę prostą swoich podgrup

(Kontynuacja seminarium z 2008-04-15)

2008-04-15 Seminarium

Hubert Przybycień

Twierdzenia o rozkładzie grupy topologicznej 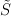$\tilde{S}$ na topologiczną sumę prostą swoich podgrup

(Kontynuacja seminarium z 2008-04-08)

2008-04-08 Seminarium

Hubert Przybycień

Twierdzenia o rozkładzie grupy topologicznej 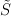$\tilde{S}$ na topologiczną sumę prostą swoich podgrup

Podczas referatu udowodnimy twierdzenie o rozkładzie grupy topologicznej $(\tilde{S},+)$ na topologiczną sumę prostą swoich podgrup: symetrycznej i asymetrycznej, w oparciu o pewne założenia dotyczące jednostajnej ciągłości dodawania oraz tzw. operatora symetrii. Ponadto podamy przykłady ilustrujące rozważane zagadnienia.

2008-04-01 Wykład im. Ambrożego Kleksa

IV Uroczysty Wykład im. Ambrożego Kleksa

profa dra Maksymiliana Paradys (Interdyscyplinarne Centrum Badań Gender Studies)

O męskiej dominacji w matematyce

Odczyt poświęcony będzie analizie problemu męskiego szowinizmu w matematyce. Zagadnienie to było dotąd rozpatrywane głównie z perspektywy historycznej, wykazując liczne przekłamania w mainstreamowych, zmaskulinizowanych źródłach, podających np. błędne informacje o tak znakomitych matematyczkach jak Euklideia, Joanna Kepler, siostry Bernoulli, Bernadeta Riemann czy Stefania Banach. Tym razem celem ataku będzie niezdobyta dotąd twierdza twierdzeń i ich dowodów. Pokażemy, jak typowo męskie cechy psychiczne odbijają się w ich sformułowaniach (co widać np. w autorytarnych określeniach typu "Niech x będzie...", nie znoszących sprzeciwu "Dowód jest zakończony", wreszcie tak charakterystycznym dla męskiej psychiki wąskim widzeniem świata: "Możliwe są jedynie dwa przypadki..."). Przeanalizujemy też wybrane dowody klasycznych twierdzeń, wykazując, że noszą wyraźne piętno męskiej indoktrynacji. Najlepszym tego przykładem jest niemal całkowite wyparcie z obecnej literatury matematycznej typowo żeńskiej metody indukcji pozaskończonej, szeroko stosowanej przez Stefanię Banach, męską metodą pochodzącą od Kuratowskiego i Zorna, w której kompleks niższości uwidacznia się w maniakalnym poszukiwaniu elementów maksymalnych.

Po odczycie będzie można nabyć publikacje oraz zabrać ulotki.

2008-04-01 Seminarium

Hubert Przybycień

O rozkładzie grupy 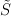$\tilde{S}$ na część symetryczną i asytmetryczną

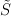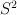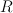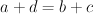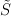Niech $(S,+)$ będzie przemienną semigrupą z zerem i prawem skreśleń. Przez $\tilde{S}$ oznaczymy zbiór $S^{2}$ , w którym wprowadzono relację równoważności $R$ taką, że $(a,b)R(c,d)$ wtedy i tylko wtedy, gdy $a+d=b+c$ . Pokażemy, iż $(\tilde{S},+)$ jest grupą i przy pewnych założeniach $\tilde{S}$ można przedstawić jako sumę prostą dwóch podgrup: symetrycznej i asymetrycznej.

2008-03-18 Seminarium

Danuta Borowska

Twierdzenia o rozkładzie domkniętego, wypukłego zbioru

(Kontynuacja seminarium z 2008-03-11)

2008-03-11 Seminarium

Danuta Borowska

Twierdzenia o rozkładzie domkniętego, wypukłego zbioru

Podczas referatu szczegółowo omówione zostanie twierdzenie Klee-Minkowskiego-Hirscha o rozkładzie domkniętego, wypukłego zbioru 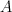$A$ na przestrzeń linearności 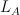$L_{A}$ , stożek asymptotyczny 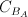$C_{B_A}$ oraz powłokę wypukłą punktów ekstremalnych zbioru 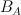$B_{A}$ , będącego przekrojem danego zbioru 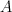$A$ oraz dopełnienia ortogonalnego przestrzeni linearności. Pokażemy również, iż powyższe twierdzenie jest uogólnieniem wielu klasycznych wyników.

2008-03-04 Seminarium

Piotr Kasprzak

Ortogonalność w sensie Birkhoffa i iloczyny półskalarne w przestrzeniach Banacha

(Kontynuacja seminarium z 2008-02-26)

2008-02-26 Seminarium

Piotr Kasprzak

Ortogonalność w sensie Birkhoffa i iloczyny półskalarne w przestrzeniach Banacha

Wprowadzimy pojęcie ortogonalności w sensie Birkhoffa oraz iloczynu półskalarnego w przestrzeni Banacha, zaprezentujemy pewne ich własności i podamy przykłady, jak również zastosowania.

2008-02-19 Seminarium

Marcin Borkowski
Ortogonalność w przestrzeniach unormowanych
(Kontynuacja seminarium z 2008-01-22)

2008-01-22 Seminarium

Marcin Borkowski
Ortogonalność w przestrzeniach unormowanych

Omówimy dwa sposoby zdefiniowania prostopadłości w przestrzeniach bez iloczynu skalarnego. Referat będzie oparty na klasycznej pracy R. C. Jamesa na ten temat.

2008-01-10 Seminarium

Wykład odbędzie się we czwartek o 12.00 w sali A1-33

prof. dr hab. Andrzej Cegielski (Wydział Matematyki, Informatyki i Ekonometrii Uniwersytetu Zielonogórskiego)

Operatory regularnie nieoddalające i ich zastosowania

2008-01-08 Seminarium

Marcin Borkowski
O pewnych twierdzeniach typu Krasnosielskiego

(Kontynuacja seminarium z 2007-12-04)