Last edit
Changed:
< Niech $$f(x,y) = 0$$ będzie rówaniem analitycznym (tzn., funkcja $$f$$ jest analityczna). Pokażemy, że jeżeli równanie ma rozwiązanie $$y(x)$$ w przestrzeni szeregów formalnych, to ma również rozwiązania analityczne rózniące się od $$y(x)$$ tylko współczynnikami przy dużych potęgach.
to
> Niech $$f(x,y) = 0$$ będzie rówaniem analitycznym (tzn. funkcja $$f$$ jest analityczna). Pokażemy, że jeżeli równanie ma rozwiązanie $$y(x)$$ w przestrzeni szeregów formalnych, to ma również rozwiązania analityczne rózniące się od $$y(x)$$ tylko współczynnikami przy dużych potęgach.
Michał Goliński
Formalne szeregi potęgowe, (cz. I)
Na seminarium omówimy następujące twierdzenie M. Artina:
Niech 203d200202424.png)
będzie rówaniem analitycznym (tzn. funkcja 
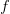jest analityczna). Pokażemy, że jeżeli równanie ma rozwiązanie 202424.png)
w przestrzeni szeregów formalnych, to ma również rozwiązania analityczne rózniące się od tylko współczynnikami przy dużych potęgach.