Last edit
Changed:
< Niech $$(S,+)$$ będzie przemienną semigrupą z zerem i prawem skreśleń. Przez $$\tilde{S}$$ oznaczymy zbiór $$S^{2}$$, w którym wprowadzono relację równoważności $$R$$ taką, że $$(a,b)R(c,d)$$ wtedy i tylko wtedy, gdy $$a+d=b+c$$. Pokażemy, iż $$(\tilde{S},+)$$ jest grupą i przy pewnych założeniach $$\tilde{S}$$ można przedstawić jako sumę prostą dwóch podgrup: części symetrycznej i asymetrycznej.
to
> Niech $$(S,+)$$ będzie przemienną semigrupą z zerem i prawem skreśleń. Przez $$\tilde{S}$$ oznaczymy zbiór $$S^{2}$$, w którym wprowadzono relację równoważności $$R$$ taką, że $$(a,b)R(c,d)$$ wtedy i tylko wtedy, gdy $$a+d=b+c$$. Pokażemy, iż $$(\tilde{S},+)$$ jest grupą i przy pewnych założeniach $$\tilde{S}$$ można przedstawić jako sumę prostą dwóch podgrup: symetrycznej i asymetrycznej.
Hubert PrzybycieńO rozkładzie grupy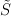 
na część symetryczną i asytmetryczną
Niech 202424.png)
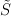będzie przemienną semigrupą z zerem i prawem skreśleń. Przez oznaczymy zbiór 
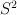, w którym wprowadzono relację równoważności 
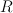taką, że R(c2cd)202424.png)
wtedy i tylko wtedy, gdy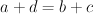 
. Pokażemy, iż 202424.png)
jest grupą i przy pewnych założeniach 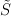można przedstawić jako sumę prostą dwóch podgrup: symetrycznej i asymetrycznej.