Oto tytuły i streszczenia seminariów z 2007 roku:

2007-12-04 Seminarium

Marcin Borkowski
O pewnych twierdzeniach typu Krasnosielskiego

W referacie udowodnimy dwa twierdzenia o punkcie stałym typu Krasnosielskiego.

2007-11-27 Seminarium

Danuta Borowska i Jerzy Grzybowski
Własność przecięć w rodzinie zbiorów domkniętych ograniczonych i wypukłych

(Kontynuacja seminarium z 2007-11-13)

2007-11-20 Seminarium

P. Kawęcki, B. Kraska, K. Majcherek, M. Zoła (referuje: B. Kraska)
(Katolicki Uniwersytet Lubelski Jana Pawła II)

Obrona odcinka

Problem referatu dotyczy zagadnienia obrony w grze różniczkowej odcinka na
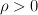płaszczyźnie z normą $\|(x_{1}, x_{2})\| = \max \{|x_{1}|, |x_{2}|\}$ . Bierze w niej udział dwóch graczy: D - obrońca oraz I - napastnik. Odcinek jest broniony przez obrońcę D. Napastnik I ma za zadanie zdobyć ten odcinek, ale musi zachować odpowiednią odległość do obrońcy nie mniejszą niż zadana dodatnia stała $\rho > 0$ . 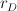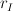Obrońca i napastnik mogą poruszać się po całej płaszczyźnie z maksymalną prędkością $r_{D}$ oraz $r_{I}$ odpowiednio, gdzie 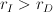$r_{I} > r_{D}$ . Zakładamy, że ruch obrońcy oraz napastnika nie jest ograniczony prawami kinematyki i dynamiki. Maksymalna długość odcinka, który może być obroniony przez obrońcę jest przedstawiona w tym referacie.

2007-11-13 Seminarium

Danuta Borowska i Jerzy Grzybowski
Własność przecięć w rodzinie zbiorów domkniętych ograniczonych i wypukłych

Przedmiotem rozważań będzie badanie zwartych wypukłych zbiorów mających następującą własność: niepuste przecięcie dowolnej rodziny translacji zbioru jest sumantem (w sensie Minkowskiego) tego zbioru. Pokażemy, że niektóre zbiory inne niż wielościany i elipsoidy, to jest kliny, tępe kliny i pewne części kuli Euklidesowej, posiadają także taką własność. Przedstawimy rodzinę wszystkich 3 wymiarowych wielościennych zbiorów, które mają tę własność. Pokażemy, że ta rodzina pokrywa się z wszystkimi trzywymiarowymi silnie monotypicznymi wielościanami.

2007-11-06 Seminarium

Marcin Borkowski
Powłoka hiperwypukła raz jeszcze

W referacie podamy warunek konieczny i dostateczny na to, by powłoka hiperwypukła podzbioru przestrzeni metrycznej hiperywpukłej była wyznaczona w sposób jednoznaczny.

2007-10-23 Seminarium

Hubert Przybycień
O przestrzeni sprzężonej do przestrzeni funkcji 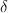$\delta$ -wypukłych

Referat oparty będzie na pracy Urbana Cegrella "On the space of 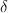$\delta$ -convex functions and its dual".

2007-10-16 Seminarium

Marcin Borkowski
Hiperwypukłość a wypukłość

Przedmiotem referatu będzie charakteryzacja tych przestrzeni Banacha, w których każdy zbiór domknięty i wypukły jest hiperwypukły oraz tych, w których zachodzi implikacja odwrotna.

2007-10-09 Seminarium

Ryszard Urbański
O minimach rodzin funkcji subliniowych

W referacie podamy warunek konieczny i dostateczny na to, by minimum skończonej ilości elementów przestrzeni Minkowskiego-Rådströma-Hörmandera należało do stożka zbiorów niepustych, ograniczonych, domkniętych i wypukłych. Zastosujemy ten wynik do wykazania warunku na to, by minimum skończenie wielu funkcji podparcia było subliniowe.

2007-05-29 Seminarium

Ryszard Urbański i Jerzy Grzybowski
Sprawozdanie z konferencji Convex and Fractal Geometry w Będlewie

2007-05-15 Seminarium

Jerzy Grzybowski
O wzroście kryształów

Przedstawimy pewien model wzrostu kryształów oraz warunek konieczny i dostateczny na znikanie ścian. Obliczymy też pochodną i zaproponujemy formułę pozwalającą wyznaczyć kształt kryształu w dowolnej chwili.

2007-05-08 Seminarium

Marcin Borkowski
Twierdzenia typu Darbo dla multifunkcji

Zaprezentujemy pewne twierdzenia typu Darbo dla operatorów wielowartościowych w przestrzeniach metrycznych hiperwypukłych.

(Kontynuacja seminarium z 2007-04-17)

2007-04-25 Seminarium

Wykład odbędzie się we środę o 12.30 w sali B3-39

prof. dr hab. Andrzej Fryszkowski (Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej)

Lemat Filipowa dla inkluzji różniczkowych wyższych rzędów

Streszczenie (pdf)

2007-04-17 Seminarium

Marcin Borkowski
Twierdzenia typu Darbo dla multifunkcji

Zaprezentujemy pewne twierdzenia typu Darbo dla operatorów wielowartościowych w przestrzeniach metrycznych hiperwypukłych.

2007-04-01 Wykład im. Ambrożego Kleksa

III Uroczysty Wykład im. prof. Ambrożego Kleksa

Herr O. Dot (gość z przyszłości - Uniwersytet Ziemi, Katera Historii Idei, rok 2612)
Wiek paradoksów. Matematyka XXI wieku

Wykład jest próbą podsumowania dorobku matematyki XXI wieku. Kilkusetletnia już perspektywa historyczna pozwala na dość obiektywną próbę ujęcia tego wieku niezwykłych paradoksów i burzliwego rozwoju. Z jednej strony, przez cały wiek XX i pierwsze dekady XXI mieliśmy do czynienia z niemal wykładniczym wzrostem liczby czasopism matematycznych, z drugiej zaś poziom wiedzy matematycznej w społeczeństwie był niemal zerowy (dość wspomnieć, że przeciętny absolwent szkoły średniej nie znał nawet tak elementarnych pojęć, jak przestrzeń Banacha, homologie symplicjalne czy graf Turána). Rosnąca już co najmniej od pierwszej połowy XX wieku świadomość przenikania się różnych gałęzi matematyki szła w parze z niezrozumiałym obecnie zaskoczeniem, jakim był klasyczny dziś dowód twierdzenia Riemanna o zerach funkcji dzeta przeprowadzony metodami teorii gier czy przepiękna teoria Nowaka-Kowalskiego, pozwalająca stosować aparat równań różniczkowych w kombinatoryce. W trakcie wykładu podejmiemy próbę rekonstrukcji sposobu myślenia XXI-wiecznych matematyków.

2007-03-28 Seminarium

Wykład odbędzie się we środę o 12.30 w sali B3-39

prof. dr hab. Tadeusz Rzeżuchowski (Wydział Matematyki i Nauk Informacyjnych Politechniki Warszawskiej)

O równoważnych inkluzjach różniczkowych i minimalnych założeniach wypukłości prawej strony

2007-03-20 Seminarium

Hubert Przybycień
O zupełności prezstrzeni Minkowskiego-Rådströma-Hörmandera

Rozpatrzmy zagadnienie zupełności przestrzeni Minkowskiego-Rådströma-Hörmandera 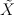$\tilde{X}$ w przypadku, gdy 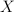$X$ jest metryzowalną przestrzenią liniowo-topologiczną.

2007-03-13 Seminarium

Ryszard Urbański i Jerzy Grzybowski
Punkty eksponowane kuli jednostkowej w przestrzeni Minkowskiego-Rådströma-Hörmandera

(Kontynuacja seminarium z 2007-03-06)

2007-03-06 Seminarium

Ryszard Urbański i Jerzy Grzybowski
Punkty ekstremalne kuli jednostkowej w przestrzeni Minkowskiego-Rådströma-Hörmandera

(Kontynuacja seminarium z 2007-02-27)

2007-02-27 Seminarium

Ryszard Urbański i Jerzy Grzybowski
Punkty ekstremalne kuli jednostkowej w przestrzeni Minkowskiego-Rådströma-Hörmandera

Podczas referatu pokażemy, że kula jednostkowa w prezstrzeni Minkowskiego-Rådströma-Hörmandera 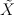$\tilde{X}$ nad dowolną przestrzenią unormowaną 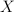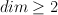$X$ , $dim \geq 2$ , posiada dokładnie dwa punkty ekstremalne. Rezultat ten jest wynikiem charakteryzacji puntów ekstremalnych dowolnego symetrycznego przedziału w kracie Minkowskiego-Rådströma-Hörmandera 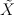$\tilde{X}$ nad dowolną przestrzenią liniowo-topologiczną Hausdorffa $X$ .

2007-02-20 Seminarium

Hubert Przybycień

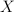2007-01-23 Seminarium

Paweł Suplicki
O funkcjach przedstawianych jako różnica dwóch funkcji wypukłych
(Kontynuacja seminarium z 2007-01-16)

2007-01-16 Seminarium

Paweł Suplicki
O funkcjach przedstawianych jako różnica dwóch funkcji wypukłych