Zakład Optymalizacji i Sterowania: 2018-10-23 Seminarium nieliniowe

Adam Nawrocki
O splocie pewnej funkcji prawie-okresowej

Dla 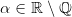$\alpha \in \mathbb R \setminus \mathbb Q$ definiujemy rodzinę funkcji

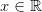$f_\alpha(x)=\frac{1}{2+\cos x +\cos(\alpha x)}$ dla $x\in \mathbb R$ .

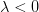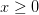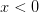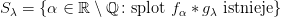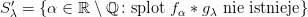Ponadto dla $\lambda<0$ niech $g(x)=e^{\lambda x}$ , jeżeli $x\geq 0$ oraz $g(x)=0$ , jeżeli $x<0$ . Wówczas zbiory $S_{\lambda}=\{\alpha \in \mathbb R \setminus \mathbb Q\colon \text {splot $f_\alpha *g_\lambda$ istnieje}\}$ oraz $S_{\lambda}^{\prime}=\{\alpha \in \mathbb R \setminus \mathbb Q\colon \text {splot $f_\alpha *g_\lambda$ nie istnieje}\}$ są gęstymi podzbiorami w 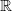$\mathbb R$ . Podczas seminarium podamy własności tych zbiorów z punktu widzenia teorii mnogości, teorii miary oraz topologii.

Seminarium wyjątkowo rozpocznie się o godzinie 10:45.