Zakład Optymalizacji i Sterowania: 2018-10-23 Nonlinear Seminar

Adam Nawrocki
Some remarks concerning the convolution of a certain almost periodic function

For 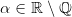$\alpha \in \mathbb R \setminus \mathbb Q$ we define the family of the functions

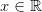$f_\alpha(x)=\frac{1}{2+\cos x +\cos(\alpha x)}$ dla $x\in \mathbb R$ .

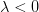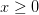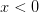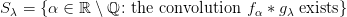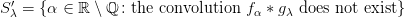Moreover for $\lambda<0$ let $g(x)=e^{\lambda x}$ if $x\geq 0$ and $g(x)=0$ if $x<0$ . Then the sets $S_{\lambda}=\{\alpha \in \mathbb R \setminus \mathbb Q\colon \text {the convolution $f_\alpha *g_\lambda$ exists}\}$ and $S_{\lambda}^{\prime}=\{\alpha \in \mathbb R \setminus \mathbb Q\colon \text {the convolution $f_\alpha *g_\lambda$ does not exist}\}$ are dense subsets of 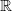$\mathbb R$ . During the seminar we give properties of these sets from the point of view of set theory, measure theory and topology.

The seminar starts at 10:45.