Albert Kubzdela
O pewnych własnościach wybranych miar niezwartości w
analizie niearchimedesowej.
Niech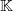 
będzie lokalnie zwartym ciałem niearchimedesowym, a 
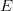niearchimedesową przestrzenią Banacha nad 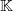. Określę niearchimedesowe odpowiedniki kilku powszechnie znanych miar niezwartości definiowanych na 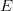, scharakteryzuję ich własności, oraz przedstawię kwantytatywne wersje kilku klasycznych twierdzeń o słabej zwartości (Twierdzenia Kreina, Gantmachera
i Grothendiecka) dla niearchimedesowych przestrzeni Banacha.