Adam Burchardt
O pewnym twierdzeniu o punkcie stałym
Podczas seminarium omówimy następujące udowodnione przez R.Cauty'ego twierdzenie o punkcie stałym, będące uogólnieniem klasycznego twierdzenia Schaudera:
Niech 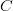 będzie wypukłym podzbiorem przestrzeni liniowo-topologicznej
będzie wypukłym podzbiorem przestrzeni liniowo-topologicznej 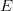 . Jeżeli
. Jeżeli 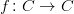 jest funkcją ciągłą oraz obraz
jest funkcją ciągłą oraz obraz 202424.png) jest zawarty w pewnym zwartym podzbiorze zbioru
jest zawarty w pewnym zwartym podzbiorze zbioru 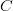 , to
, to 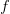 ma punkt stały.
ma punkt stały.
Referat oparty jest na pracy: R. Cauty, Solution du problème de point fixe de Schauder, Fund.Math. 170 (2001), ss. 231-246.