Here are the titles and abstracts of the seminars which were held in 2012:

2012-12-18 Nonlinear Seminar

Monika Naskręcka
Homeomorphism of the space of polynomials and the space of their roots

(Continuation of the 2012-12-11 Nonlinear Seminar)

2012-12-11 Nonlinear Seminar

Monika Naskręcka
Homeomorphism of the space of polynomials and the space of their roots

During this seminar an elementary, topological proof of continuity of the roots of complex polynomials with respect to their roots will be shown. For normed polynomials with complex coefficients and properly defined metric spaces this theorem can be expressed as a homeomorphism of corresponding metric spaces of coeffecients and roots.

2012-12-04 Nonlinear Seminar

Piotr Maćkowiak
The existence of surplus demand function zeros

(Continuation of the 2012-10-09 and 2012-10-16 Nonlinear Seminars.)

2012-11-27 Nonlinear Seminar

Piotr Zdanowicz
Basic properties of formal series

(Continuation of the 2012-11-20 Nonlinear Seminar)

2012-11-20 Nonlinear Seminar

Piotr Zdanowicz
Basic properties of formal series

2012-11-13 Nonlinear Seminar

Piotr Kasprzak
On a certain class of functions of 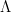$\Lambda$ -bounded variation

(Continuation of the 2012-10-30 Nonlinear Seminar)

2012-11-06 Nonlinear Seminar

The seminar will take place at 8:30 in the Faculty Council meeting room (A1-33/34)

Justyna Signerska
Firing map for integrate-and-fire models with an almost periodic drive

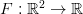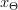Consider the integrate-and-fire system $\dot{x}=F(t,x)$ , $F:\mathbb{R}^2\to \mathbb{R}$ , in which the continuous dynamics is interrupted by the threshold-and-reset behaviour: $\lim_{t\to s^+}x(t)=x_r$ if $x(s)=x_{\Theta}$ , meaning that once the value of a dynamical variable reaches a certain threshold $x_{\Theta}$ it is immediately reset to a resting value 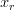$x_r$ and the system evolves again according to the differential equation. 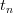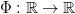The question is to describe the time series of consecutive resets (spikes) $t_n$ as iterations $\Phi^n(t_0)$ of some map $\Phi:\mathbb{R}\to \mathbb{R}$ , called the firing map, and the sequence of interspike-intervals 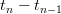$t_n-t_{n-1}$ as a sequence of displacements $\Phi^n(t_0)-\Phi^{n-1}(t_0)$ along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.

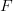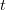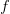However, so far properties of the firing map were analytically investigated only for the function $F$ , which is smooth enough and often also periodic in $t$ . We present a complete description of the properties of the firing map arising from the most popular models: $\dot{x}=-\sigma x +f(t)$ (Leaky Integrate-and-Fire) and $\dot{x}=f(t)$ (Perfect Integrator), when the function $f$ is only locally integrable and/or almost periodic. In particular, we prove that a Stepanov almost periodic function 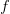$f$ induces the firing map 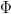$\Phi$ with the uniformly (Bohr) almost periodic displacement 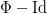$\Phi-\textrm{Id}$ . In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.

2012-10-30 Nonlinear Seminar

Piotr Kasprzak
On a certain class of functions of 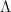$\Lambda$ -bounded variation

During the seminar we are going to define a certain class of functions of 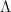$\Lambda$ -bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.

2012-10-23 Nonlinear Seminar

Piotr Kasprzak
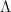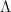On a certain class of functions of $\Lambda$ -bounded variation

2012-10-16 Nonlinear Seminar

Piotr Maćkowiak
The existence of surplus demand function zeros

(Continuation of the 2012-10-09 Nonlinear Seminar)

2012-10-09 Nonlinear Seminar

Piotr Maćkowiak
The existence of surplus demand function zeros

2012-05-29 Nonlinear Seminar

Piotr Kasprzak
On a certain class of functions of bounded variation

(Continuation of the 2012-04-24 Nonlinear Seminar)

2012-05-22 Nonlinear Seminar

Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
(Continuation of the 2012-05-08 Nonlinear Seminar)

2012-05-15 Nonlinear Seminar

Michał Burzyński
Alternative proofs of Arrow's impossibility theorem

(Continuation of the 2012-05-08 Nonlinear Seminar)

2012-05-08 Nonlinear Seminar

Michał Burzyński
Alternative proofs of Arrow's impossibility theorem

Arrow's impossibility theorem states, that if there are at least three potential social states, there is no such social welfare function 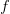$f$ (that describes the society as a whole with given individual preferences), which satisfies the following four conditions: 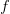$f$ has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle; 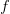$f$ satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function 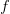$f$ there is no dictatorship. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.

2012-04-24 Nonlinear Seminar

Piotr Kasprzak
On a certain class of functions of bounded variation

We are going to define a relatively large class of functions of bounded variation defined on an open subset of 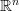$\mathbb R^n$ , which in particular contains the Sobolev space $W^{1,1}(\Omega)$ . Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.

2012-04-03 Nonlinear Seminar

Piotr Kasprzak
On the compactness criterion in the space of bounded real-valued continuous functions defined on a non-compact domain

During the seminar we are going to discuss a certain compactness criterion in the space of bounded real-valued continuous functions defined on a non-compact domain related to the well-known Arzela-Ascoli theorem.

2012-03-27 Nonlinear Seminar

Piotr Maćkowiak
Exploding points

We will present and prove theorem of the exploding point. This theorem states that for any function defined on a compact set X, containing the cube K centered at zero in its interior, with values in X\K, which is the identity on the boundary of the set X, there exists a point c in X, that in any surroundings of c, there is a point x such that the value of f(x) and f(c) are located on opposite walls of the cube K.

2012-03-20 Nonlinear Seminar

Adam Nawrocki
An Application of Continued Fractions

During this seminar we will discuss basic properties of Continued Fractions. Next we shall use Continued Fractions to calculate the limit of:
$\lim_{x\rightarrow\infty}\frac{e^{-x}}{2+\cos(x)+\cos(\sqrt{2}x)}$

(Continuation of the 2012-03-13 Nonlinear Seminar)

2012-03-13 Nonlinear Seminar

Adam Nawrocki
An Application of Continued Fractions

2012-03-06 Nonlinear Seminar

Marcin Wachowiak
Applications of Theorem Hopf-Lefschetz fixed point
(Continuation of the 2011-11-22 Nonlinear Seminar and 2011-11-29 Nonlinear Seminar and 2011-12-06 Nonlinear Seminar).

2012-02-28 Nonlinear Seminar

Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar, 2012-01-03 Nonlinear Seminar, 2012-02-14 Nonlinear Seminar and 2012-02-21 Nonlinear Seminar).

2012-02-21 Nonlinear Seminar

Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar and 2012-01-03 Nonlinear Seminar and 2012-02-14 Nonlinear Seminar).

2012-02-14 Nonlinear Seminar

Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar and 2012-01-03 Nonlinear Seminar).

2012-01-24 Nonlinear Seminar

Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
(Continuation of the 2012-01-10 Nonlinear Seminar and 2012-01-17 Nonlinear Seminar).

2012-01-17 Nonlinear Seminar

Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
(Continuation of the 2012-01-10 Nonlinear Seminar).

2012-01-10 Nonlinear Seminar

Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.

We are going to consider linear differential and nonlinear integral equations in the
spaces of functions of Lambda-bounded variation. We will state the existence and the existence and uniqueness results in this space as well as in its subspace consisting of contninuous functions of Lambda-bounded variation.

2012-01-03 Nonlinear Seminar

Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar).