Optimization and Control Theory Department: 2012-11-06 Seminarium nieliniowe

Justyna Singerska
Analiza modelu neuronu z prawie okresową funkcją wejścia.

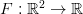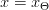Rozważmy układ typu integrate-and-fire $\dot{x}=F(t,x)$ , $F:\mathbb{R}^2\to \mathbb{R}$ , w którym ciągła dynamika jest zaburzona w następujący sposób: $\lim_{t\to s^+}x(t)=x_r$ jeśli $x(s)=x_{\Theta}$ , tj. jeśli zmienna dynamiczna $x(t)$ osiąga pewną ustaloną wartość progową $x=x_{\Theta}$ , jest natychmiast ,,resetowana do wartości spoczynkowej 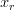$x_r$ i układ ewoluuje od nowa zgodnie z równaniem różniczkowym itd. Pytanie: W jaki sposób opisać szereg czasowy kolejnych resetowań (ang. 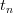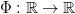spikes) $t_n$ jako kolejne iteracje $\Phi^n(t_0)$ pewnego odwzorowania $\Phi:\mathbb{R}\to \mathbb{R}$ , zwanego firing map, a ciąg interspike-intervals/ 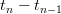$t_n-t_{n-1}$ jako ciąg przemieszczeń $\Phi^n(t_0)-\Phi^{n-1}(t_0)$ wzdłuż trajektorii tego odwzorowania? Problem ten pojawia się m.in. w modelowaniu aktywności komórek nerwowych.

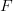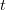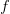Jednakże dotychczas właściwości firing map były badane analitycznie jedynie przy założeniu, że funkcja $F$ jest dostatecznie gładka i często także okresowa względem zmiennej $t$ . My prezentujemy pełny opis własności firing map dla najpopularniejszych modeli $\dot{x}=-\sigma x+f(t)$ (tzw. Leaky Integrate-and-Fire) oraz $\dot{x}=f(t)$ (tzw. Perfect Integrator), gdzie funkcja $f$ jest jedynie lokalnie całkowalna i/lub prawie okresowa. W szczególności okazuje się, że 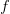$f$ prawie okresowa w sensie Stepanova daje firing map 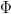$\Phi$ z przemieszczeniem 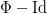$\Phi-\textrm{Id}$ prawie okresowym w sensie Bohra, co stanowi wstęp do formalnej analizy ciągu interspike-intervals w przypadku prawie okresowym.