Optimization and Control Theory Department: 2012-11-06 Nonlinear Seminar

Justyna Singerska
Firing map for integrate-and-fire models with an almost periodic drive

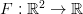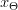Consider the integrate-and-fire system $\dot{x}=F(t,x)$ , $F:\mathbb{R}^2\to \mathbb{R}$ , in which the continuous dynamics is interrupted by the threshold-and-reset behaviour: $\lim_{t\to s^+}x(t)=x_r$ if $x(s)=x_{\Theta}$ , meaning that once the value of a dynamical variable reaches a certain threshold $x_{\Theta}$ it is immediately reset to a resting value 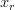$x_r$ and the system evolves again according to the differential equation. 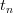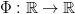The question is to describe the time series of consecutive resets (spikes) $t_n$ as iterations $\Phi^n(t_0)$ of some map $\Phi:\mathbb{R}\to \mathbb{R}$ , called the firing map, and the sequence of interspike-intervals 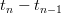$t_n-t_{n-1}$ as a sequence of displacements $\Phi^n(t_0)-\Phi^{n-1}(t_0)$ along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.

However, so far properties of the firing map were analytically investigated only for the function 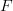$F$ , which is smooth enough and often also periodic in 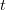$t$ . We present a complete description of the properties of the firing map arising from the most popular models: $\dot{x}=-\sigma x +f(t)$ (Leaky Integrate-and-Fire) and $\dot{x}=f(t)$ (Perfect Integrator), when the function $f$ is only locally integrable and/or almost periodic. 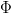In particular, we prove that a Stepanov almost periodic function $f$ induces the firing map $\Phi$ with the uniformly (Bohr) almost periodic displacement 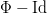$\Phi-\textrm{Id}$ . In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.