Xiao-Xiong Gan
(Mathematics Department, Morgan State University, Baltimore, USA)
Formal Power Series and the Boundary Convergence of Power Series
The behaviour of power series on boundary of convergence domain has been an interesting topic since power series was introduced. For example,
203d205csum_7bn3d17d5e7b5cinfty7d5cdfrac7b(-1)5en7d7bn7dx5en202424.png)
converges on ![$$ (-1,1] $$](https://octd.wmi.amu.edu.pl/latex/242420(-12c15d202424.png) but diverges at
but diverges at 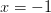 , and
, and 20202424.png) diverges at both
diverges at both 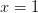 and
and 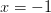 . The composition of formal power series has been an important part of the formal power series theory. We introduce some relationship between these two subjects and provide a condition for convergence of a power series at every point in its interval of convergence, including endpoints or boundary points.
. The composition of formal power series has been an important part of the formal power series theory. We introduce some relationship between these two subjects and provide a condition for convergence of a power series at every point in its interval of convergence, including endpoints or boundary points.
The seminar will take place at 9:00.