Last edit
Changed:
< W referacie pokażemy, że prawie okresowe w sensie Lewitana (w skrócie: LAP) rozwiązania równania $$y(x)=\lambda y(x)+f(x)$$ zazwyczaj można wyrazić za pomocą splotu. Pokażemy, że w ten sposób można otrzymać nieograniczone rowiązania LAP. Podamy również przykład pokazujący, że splot nie zawsze jest dobrym narzędziem do szukania rozwiązań LAP.
to
> W referacie pokażemy, że prawie okresowe w sensie Lewitana (w skrócie: LAP) rozwiązania równania $$y$$'$$(x)=\lambda y(x)+f(x)$$ zazwyczaj można wyrazić za pomocą splotu. Pokażemy, że w ten sposób można otrzymać nieograniczone rowiązania LAP. Podamy również przykład pokazujący, że splot nie zawsze jest dobrym narzędziem do szukania rozwiązań LAP.
Adam Nawrocki
Prawie okresowe w sensie Lewitana rozwiązania pewnego liniowego równania różniczkowego
W referacie pokażemy, że prawie okresowe w sensie Lewitana (w skrócie: LAP) rozwiązania równania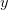 
'3d5clambda20y(x)2bf(x)202424.png)
zazwyczaj można wyrazić za pomocą splotu. Pokażemy, że w ten sposób można otrzymać nieograniczone rowiązania LAP. Podamy również przykład pokazujący, że splot nie zawsze jest dobrym narzędziem do szukania rozwiązań LAP.