Last edit
Changed:
< Let $$ \mathbb{K} $$ be a locally compact non-Archimedean field, and $$ E $$ non-Archimedean Banach space over $$ \mathbb{K} $$. We define non-Archimedean equivalents of several well-known measures of non-compactness defined on $$ E $$, we characterize their properties and we present quantitative versions of several classic statements on weak compactness (theorems of Krein, Gantmacher and Grothendieck) for non-Archimedean Banach spaces.
to
> Let $$ \mathbb{K} $$ be a locally compact non-Archimedean field, and $$ E $$ a non-Archimedean Banach space over $$ \mathbb{K} $$. We define non-Archimedean equivalents of several well-known measures of non-compactness defined on $$ E $$, we describe their properties and we present quantitative versions of several classic statements on weak compactness (theorems of Krein, Gantmacher and Grothendieck) for non-Archimedean Banach spaces.
Albert Kubzdela
On some properties of some measure of non-compactness in non-Archimedean analysis
Let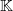 
be a locally compact non-Archimedean field, and 
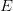a non-Archimedean Banach space over 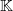. We define non-Archimedean equivalents of several well-known measures of non-compactness defined on 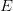, we describe their properties and we present quantitative versions of several classic statements on weak compactness (theorems of Krein, Gantmacher and Grothendieck) for non-Archimedean Banach spaces.