Optimization and Control Theory Department: 2014-03-11 Seminarium nieliniowe

Last edit

Changed:

< Wiadomo, że funkcja ciągła $$f\colon \mathbb{R}\to \mathbb{R}$$, spełniająca lokalny warunek Lipschitza, złożona z funkcją $$x(t)$$ o ograniczonej wariacji daje również funkcję $$(f\circ x)(t)$$ o ograniczonej wariacji. W naturalny sposób pojawia się w tym miejscu pytanie o ciągłość takiego operatora suprepozycji $$F \colon BV[0,1]\to BV[0,1]$$. Omówione zostaną pewne przypadki, w których można pokazać, że wspomniany operator jest ciągły. Podane zostaną również pewne znane uogólnienia pojęcia wariacji funkcji prowadzące do definicji przestrzeni Banacha $$E$$ zawierających przestrzeń $$BV[0,1]$$. W pewnych sytuacjach można również pokazać ciągłość operatora superpozycji $$F \colon BV[0,1]\to E$$.

to

> Wiadomo, że funkcja ciągła $$f\colon \mathbb{R}\to \mathbb{R}$$, spełniająca lokalny warunek Lipschitza, złożona z funkcją $$x(t)$$ o ograniczonej wariacji daje również funkcję $$(f\circ x)(t)$$ o ograniczonej wariacji. W naturalny sposób pojawia się w tym miejscu pytanie o ciągłość takiego operatora superpozycji $$F \colon BV[0,1]\to BV[0,1]$$. Omówione zostaną pewne przypadki, w których można pokazać, że wspomniany operator jest ciągły. Podane zostaną również pewne znane uogólnienia pojęcia wariacji funkcji prowadzące do definicji przestrzeni Banacha $$E$$ zawierających przestrzeń $$BV[0,1]$$. W pewnych sytuacjach można również pokazać ciągłość operatora superpozycji $$F \colon BV[0,1]\to E$$.

Dr Jacek Gulgowski
(Instytut Matematyki, Uniwersytet Gdański)
O ciągłości operatora superpozycji w przestrzeniach funkcji o ograniczonej wariacji

Wiadomo, że funkcja ciągła 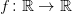$f\colon \mathbb{R}\to \mathbb{R}$ , spełniająca lokalny warunek Lipschitza, złożona z funkcją $x(t)$ o ograniczonej wariacji daje również funkcję $(f\circ x)(t)$ o ograniczonej wariacji. W naturalny sposób pojawia się w tym miejscu pytanie o ciągłość takiego operatora superpozycji $F \colon BV[0,1]\to BV[0,1]$ . Omówione zostaną pewne przypadki, w których można pokazać, że wspomniany operator jest ciągły. 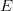Podane zostaną również pewne znane uogólnienia pojęcia wariacji funkcji prowadzące do definicji przestrzeni Banacha $E$ zawierających przestrzeń $BV[0,1]$ . W pewnych sytuacjach można również pokazać ciągłość operatora superpozycji $F \colon BV[0,1]\to E$ .