Last edit
Changed:
< Justyna Singerska
to
> Justyna Signerska
The seminar will take place at 8:30 in the Faculty Council meeting room (A1-33/34)
Justyna Signerska
Firing map for integrate-and-fire models with an almost periodic drive
Consider the integrate-and-fire system 202424.png) ,
, 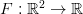 , in which the continuous dynamics is interrupted by the threshold-and-reset behaviour:
, in which the continuous dynamics is interrupted by the threshold-and-reset behaviour: 3dx_r202424.png) if
if 3dx_7b5cTheta7d202424.png) , meaning that once the value of a dynamical variable reaches a certain threshold
, meaning that once the value of a dynamical variable reaches a certain threshold 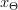 it is immediately reset to a resting value
it is immediately reset to a resting value 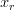 and the system evolves again according to the differential equation. The question is to describe the time series of consecutive resets (spikes)
and the system evolves again according to the differential equation. The question is to describe the time series of consecutive resets (spikes) 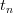 as iterations
as iterations 202424.png) of some map
of some map 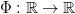 , called the firing map, and the sequence of interspike-intervals
, called the firing map, and the sequence of interspike-intervals 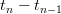 as a sequence of displacements
as a sequence of displacements -5cPhi5e7bn-17d(t_0)202424.png) along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.
along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.
However, so far properties of the firing map were analytically investigated only for the function 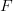 , which is smooth enough and often also periodic in
, which is smooth enough and often also periodic in 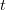 . We present a complete description of the properties of the firing map arising from the most popular models:
. We present a complete description of the properties of the firing map arising from the most popular models: 202424.png) (Leaky Integrate-and-Fire) and
(Leaky Integrate-and-Fire) and 202424.png) (Perfect Integrator), when the function
(Perfect Integrator), when the function 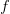 is only locally integrable and/or almost periodic. In particular, we prove that a Stepanov almost periodic function
is only locally integrable and/or almost periodic. In particular, we prove that a Stepanov almost periodic function 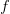 induces the firing map
induces the firing map 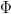 with the uniformly (Bohr) almost periodic displacement
with the uniformly (Bohr) almost periodic displacement 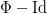 . In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.
. In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.