Last edit
Changed:
< Twierdzenie Arrowa o Niemożliwości orzeka, iż w przypadku istnienia co najmniej trzech potencjalnych stanów społecznych, nie istnieje taka społeczna funkcja bogactwa $$f$$ (opisująca preferencje społeczeństwa jako całości przy danych indywidualnych preferencjach), która spełnia cztery warunki: $$f$$ posiada nieograniczoną dziedzinę; silna relacja preferencji społecznych spełnia słabą zasadę Pareto; $$f$$ spełnia własność niezależność nieistotnych alternatyw oraz w społeczeństwie o preferencjach opisanych funkcją $$f$$ nie występuje. Oryginalny dowód K. Arrowa składa się z dwóch kroków: pokazania istnienia jednostki decydującej oraz udowodnienia, że musi być ona dyktatorem. Pierwszy z alternatywnych dowodów opiera się na wykorzystaniu preferencji Condorcet. Drugi stosuje krok pierwszy z dowodu Arrowa i wskazuje, że wszystkie decyzje społeczne podejmowane są w identyczny sposób. Ostatni dowód ma charakter graficzny.
to
> Twierdzenie Arrowa o Niemożliwości orzeka, iż w przypadku istnienia co najmniej trzech potencjalnych stanów społecznych, nie istnieje taka społeczna funkcja bogactwa $$f$$ (opisująca preferencje społeczeństwa jako całości przy danych indywidualnych preferencjach), która spełnia cztery warunki: $$f$$ posiada nieograniczoną dziedzinę; silna relacja preferencji społecznych spełnia słabą zasadę Pareto; $$f$$ spełnia własność niezależności nieistotnych alternatyw oraz w społeczeństwie o preferencjach opisanych funkcją $$f$$ nie występuje dyktator. Oryginalny dowód K. Arrowa składa się z dwóch kroków: pokazania istnienia jednostki decydującej oraz udowodnienia, że musi być ona dyktatorem. Pierwszy z alternatywnych dowodów opiera się na wykorzystaniu preferencji Condorcet. Drugi stosuje krok pierwszy z dowodu Arrowa i wskazuje, że wszystkie decyzje społeczne podejmowane są w identyczny sposób. Ostatni dowód ma charakter graficzny.
Michał Burzyński
Alternatywne dowody Twierdzenia Arrowa o Niemożliwości.
Twierdzenie Arrowa o Niemożliwości orzeka, iż w przypadku istnienia co najmniej trzech potencjalnych stanów społecznych, nie istnieje taka społeczna funkcja bogactwa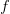 
(opisująca preferencje społeczeństwa jako całości przy danych indywidualnych preferencjach), która spełnia cztery warunki: 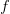posiada nieograniczoną dziedzinę; silna relacja preferencji społecznych spełnia słabą zasadę Pareto; 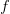spełnia własność niezależności nieistotnych alternatyw oraz w społeczeństwie o preferencjach opisanych funkcją 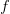nie występuje dyktator. Oryginalny dowód K. Arrowa składa się z dwóch kroków: pokazania istnienia jednostki decydującej oraz udowodnienia, że musi być ona dyktatorem. Pierwszy z alternatywnych dowodów opiera się na wykorzystaniu preferencji Condorcet. Drugi stosuje krok pierwszy z dowodu Arrowa i wskazuje, że wszystkie decyzje społeczne podejmowane są w identyczny sposób. Ostatni dowód ma charakter graficzny.