Last edit
Changed:
< Arrow's impossibility theorem states, that if there are at least three potential social conditions, there is no such social welfare function $$f$$ (which describes the society as a whole with given individual preferences), which satisfies the following four conditions: $$f$$ has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle; $$f$$ satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function $$f$$ there is no dictator. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.
to
> Arrow's impossibility theorem states, that if there are at least three potential social states, there is no such social welfare function $$f$$ (that describes the society as a whole with given individual preferences), which satisfies the following four conditions: $$f$$ has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle; $$f$$ satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function $$f$$ there is no dictatorship. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.
Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
Arrow's impossibility theorem states, that if there are at least three potential social states, there is no such social welfare function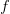 
(that describes the society as a whole with given individual preferences), which satisfies the following four conditions: 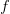has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle; 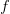satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function 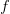there is no dictatorship. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.