Last edit
Changed:
< We are going to define a relatively large class of functions of bounded variation defined on an open subset
< of $$\mathbb R^n$$, which in particular contains the Sobolev space $$W^{1,1}(\Omega)$$. Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.
to
> We are going to define a relatively large class of functions of bounded variation defined on an open subset of $$\mathbb R^n$$, which in particular contains the Sobolev space $$W^{1,1}(\Omega)$$. Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.
Piotr Kasprzak
On a certain class of functions of bounded variation
We are going to define a relatively large class of functions of bounded variation defined on an open subset of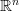 
, which in particular contains the Sobolev space 202424.png)
. Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.