Last edit
Changed:
< The talk is based on the following paper: R. Cauty, //Solution du problème de point fi xe de Schauder//, Fund. Math. **170** (2001), 231-246.
to
> The talk is based on the following paper: R. Cauty, //Solution du problème de point fixe de Schauder//, Fund. Math. **170** (2001), 231-246.
Adam Burchardt
Schauder fixed point, revisited
During the seminar we are going to discuss the following generalization of the classical Schauder fixed point theorem due to R. Cauty:
Let 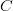 be a convex subset of a topological vector space
be a convex subset of a topological vector space 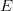 . If
. If 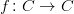 is a continuous function such that
is a continuous function such that 202424.png) is contained in a compact subset of
is contained in a compact subset of 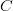 , then
, then 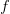 has a fixed point.
has a fixed point.
The talk is based on the following paper: R. Cauty, Solution du problème de point fixe de Schauder, Fund. Math. 170 (2001), 231-246.