Last edit
Changed:
< Podczas referatu przedstawimy m.in. pewne twierdzenia o przedłużaniu dla multifunkcji. Kluczową rolę w dowodach omawianych twierdzeń odgrywać będzie zastosowanie twierdzenia o zanurzeniu stożka $$B(X)$$ niepustych, domkniętych, ograniczonych oraz wypukłych podzbiorów przestrzeni unormowanej $$X$$ w pewną przestrzeń Banacha. Referat będzie oparty na pracy Anny Kuci //Applications of the Radström-Hörmander Embedding Theorem to Multifunctions//, Bull. Acad. Pol. Sci. Math. **53** (3) (2005), 259-271.
to
> Podczas referatu przedstawimy m.in. pewne twierdzenia o przedłużaniu dla multifunkcji. Kluczową rolę w dowodach omawianych wyników odgrywać będzie zastosowanie twierdzenia o zanurzeniu stożka $$B(X)$$ niepustych, domkniętych, ograniczonych oraz wypukłych podzbiorów przestrzeni unormowanej $$X$$ w pewną przestrzeń Banacha. Referat będzie oparty na pracy Anny Kuci //Applications of the Radström-Hörmander Embedding Theorem to Multifunctions//, Bull. Acad. Pol. Sci. Math. **53** (3) (2005), 259-271.
Piotr Kasprzak
Zastosowanie stożka 202424.png)
w teorii multifunkcji
Podczas referatu przedstawimy m.in. pewne twierdzenia o przedłużaniu dla multifunkcji. Kluczową rolę w dowodach omawianych wyników odgrywać będzie zastosowanie twierdzenia o zanurzeniu stożka niepustych, domkniętych, ograniczonych oraz wypukłych podzbiorów przestrzeni unormowanej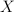 
w pewną przestrzeń Banacha. Referat będzie oparty na pracy Anny Kuci Applications of the Radström-Hörmander Embedding Theorem to Multifunctions, Bull. Acad. Pol. Sci. Math. 53 (3) (2005), 259-271.