Last edit
Changed:
< Splot funkcji całkowalnych w sensie Lebesgue'a jest klasycznym pojęciem, którego przeniesienie na grunt teorii całki nieabsolutnie zbieżnej napotyka na zaskakujące trudności. W referacie przedstawimy niektóre z tych problemów oraz przedstawimy kontrprzykłady pokazujące, że splot zdefiniowany przy użyciu całki Henstocka-Kurzweila nie ma własności analogicznych do przypadku $$L^1$$.
to
> Splot funkcji całkowalnych w sensie Lebesgue'a jest klasycznym pojęciem, którego przeniesienie na grunt teorii całek nieabsolutnie zbieżnych napotyka na zaskakujące trudności. W referacie przedstawimy niektóre z tych problemów oraz przedstawimy kontrprzykłady pokazujące, że splot zdefiniowany przy użyciu całki Henstocka-Kurzweila nie ma własności analogicznych do przypadku $$L^1$$.
Marcin Borkowski
O pewnych problemach związanych ze splotem funkcji
Splot funkcji całkowalnych w sensie Lebesgue'a jest klasycznym pojęciem, którego przeniesienie na grunt teorii całek nieabsolutnie zbieżnych napotyka na zaskakujące trudności. W referacie przedstawimy niektóre z tych problemów oraz przedstawimy kontrprzykłady pokazujące, że splot zdefiniowany przy użyciu całki Henstocka-Kurzweila nie ma własności analogicznych do przypadku 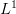 .
.