Last edit
Changed:
< //The seminar will be held at 9.00.//
to
> //The seminar will be held at 9.00 in A1-33.//
prof. dr hab. Tadeusz Rzeżuchowski (The Faculty of Mathematics and Information Science at the Warsaw University of Technology)
Demyanov metric in the family of convex bounded sets
The seminar will be held at 9.00 in A1-33.
Let  be a linear and continuous functional
be a linear and continuous functional  and
and 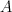 a convex bounded subset of a linear space
a convex bounded subset of a linear space 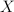 . We call the set
. We call the set 3d5csup_7by5cin20A7df(y)5c7d202424.png) the face of
the face of 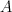 supported by the function
supported by the function  and denote it by
and denote it by 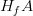 . If
. If 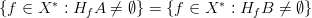 , we define the Demyanov distance between the sets
, we define the Demyanov distance between the sets 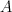 and
and 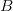 as
as 202424.png) , where
, where 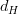 is the usual Hausdorff metric.
is the usual Hausdorff metric.