Last edit
Changed:
< Podczas referatu udowodnimy twierdzenie o rozkładzie grupy topologicznej $$(\tilde{S},+)$$ na topologiczną sumę prostą swoich podgrup: symetrycznej i asymetrycznej, w oparciu o pewne założenia dotyczące jednostajnej ciągłości dodawania oraz tzw. operatora symetrii. Ponadto podamy przykłady ilustrujące rozważane zagadnienia.
to
> Podczas referatu udowodnimy twierdzenie o rozkładzie grupy topologicznej $$(\tilde{S},+)$$ na topologiczną sumę prostą swoich podgrup: symetrycznej i asymetrycznej, w oparciu o pewne założenia dotyczące jednostajnej ciągłości dodawania oraz tzw. operatora symetrii. Ponadto podamy przykłady ilustrujące rozważane zagadnienia.
Hubert PrzybycieńTwierdzenia o rozkładzie grupy topologicznej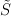 
na topologiczną sumę prostą swoich podgrup
Podczas referatu udowodnimy twierdzenie o rozkładzie grupy topologicznej 202424.png)
na topologiczną sumę prostą swoich podgrup: symetrycznej i asymetrycznej, w oparciu o pewne założenia dotyczące jednostajnej ciągłości dodawania oraz tzw. operatora symetrii. Ponadto podamy przykłady ilustrujące rozważane zagadnienia.