Last edit
Changed:
< Given a commutative semigroup with the neutral element and the cancellation law $$(S,+)$$, denote by $$\tilde{S}$$ the set $$S^{2}$$ with the equivalence relation $$R$$ such that $$(a,b)R(c,d)$$ if and only if $$a+d=b+c$$. We will show that under some assumptions it is possible to decompose $$\tilde{S}$$ into a direct sum of two subgroups: symmetric and asymmetric one.
to
> Given a commutative semigroup with the neutral element and the cancellation law $$(S,+)$$, denote by $$\tilde{S}$$ the set $$S^{2}$$ with the equivalence relation $$R$$ such that $$(a,b)R(c,d)$$ if and only if $$a+d=b+c$$. We will show that $$(\tilde{S},+)$$ is a group and under some assumptions it is possible to decompose $$\tilde{S}$$ into a direct sum of two subgroups: symmetric and asymmetric one.
Hubert PrzybycieńOn a direct sum decomposition of a group 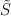
Given a commutative semigroup with the neutral element and the cancellation law 202424.png) , denote by
, denote by 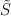 the set
the set 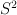 with the equivalence relation
with the equivalence relation 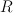 such that
such that R(c2cd)202424.png) if and only if
if and only if 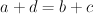 . We will show that
. We will show that 202424.png) is a group and under some assumptions it is possible to decompose
is a group and under some assumptions it is possible to decompose 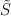 into a direct sum of two subgroups: symmetric and asymmetric one.
into a direct sum of two subgroups: symmetric and asymmetric one.