Optimization and Control Theory Department: 2007-11-20 Seminarium

Last edit

Changed:

< płaszczyźnie z normą $$\|(x_{1}, x_{2})\| = max \{|x_{1}|, |x_{2}|\}$$. Bierze w niej udział dwóch graczy: **D** - obrońca oraz **I** - napastnik. Odcinek jest broniony przez obrońcę **D**. Napastnik **I** ma za zadanie zdobyć ten odcinek, ale musi zachować odpowiednią odległość do obrońcy nie mniejszą niż zadana dodatnia stała $$\rho > 0$$. Obrońca i napastnik mogą poruszać się po całej płaszczyźnie z maksymalną prędkością $$r_{D}$$ oraz $$r_{I}$$ odpowiednio, gdzie $$r_{I} > r_{D}$$. Zakładamy, że ruch obrońcy oraz napastnika nie jest ograniczony prawami kinematyki i dynamiki. Maksymalna długość odcinka, który może być obroniony przez obrońcę jest przedstawiona w tym referacie.

to

> płaszczyźnie z normą $$\|(x_{1}, x_{2})\| = \max \{|x_{1}|, |x_{2}|\}$$. Bierze w niej udział dwóch graczy: **D** - obrońca oraz **I** - napastnik. Odcinek jest broniony przez obrońcę **D**. Napastnik **I** ma za zadanie zdobyć ten odcinek, ale musi zachować odpowiednią odległość do obrońcy nie mniejszą niż zadana dodatnia stała $$\rho > 0$$. Obrońca i napastnik mogą poruszać się po całej płaszczyźnie z maksymalną prędkością $$r_{D}$$ oraz $$r_{I}$$ odpowiednio, gdzie $$r_{I} > r_{D}$$. Zakładamy, że ruch obrońcy oraz napastnika nie jest ograniczony prawami kinematyki i dynamiki. Maksymalna długość odcinka, który może być obroniony przez obrońcę jest przedstawiona w tym referacie.

P. Kawęcki, B. Kraska, K. Majcherek, M. Zoła (referuje: B. Kraska)
(Katolicki Uniwersytet Lubelski Jana Pawła II)

Obrona odcinka

Problem referatu dotyczy zagadnienia obrony w grze różniczkowej odcinka na
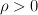płaszczyźnie z normą $\|(x_{1}, x_{2})\| = \max \{|x_{1}|, |x_{2}|\}$ . Bierze w niej udział dwóch graczy: D - obrońca oraz I - napastnik. Odcinek jest broniony przez obrońcę D. Napastnik I ma za zadanie zdobyć ten odcinek, ale musi zachować odpowiednią odległość do obrońcy nie mniejszą niż zadana dodatnia stała $\rho > 0$ . 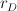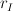Obrońca i napastnik mogą poruszać się po całej płaszczyźnie z maksymalną prędkością $r_{D}$ oraz $r_{I}$ odpowiednio, gdzie 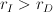$r_{I} > r_{D}$ . Zakładamy, że ruch obrońcy oraz napastnika nie jest ograniczony prawami kinematyki i dynamiki. Maksymalna długość odcinka, który może być obroniony przez obrońcę jest przedstawiona w tym referacie.