Last edit
Changed:
< Niech $$X$$ będzie przestrzenią Banacha nad $$\mathbb{R}$$ a $$Y\subset X$$ jej podprzestrzenią domkniętą. Oznaczmy symbolem $$\mathcal{P}(X,Y)$$ wszystkie rzutowania liniowe i ciągłe z $$X$$ na $$Y$$. Niech $$\lambda(Y,X)=\inf\{\|P\|:P\in\mathcal{P}(X,Y)\}$$. Dla $$n$$-wymiarowej przestrzeni Banacha $$Y$$ niech $$\lambda(Y) = \sup \{ \lambda(Y,X): Y \subset X \}$$. Stała $$\lambda(Y)$$ nazywana jest w literaturze //absolutną stałą projekcji//. Jest znanym faktem, że dla $$n$$-wymiarowej przestrzeni Banacha $$Y$$, $$\lambda(Y) = \lambda(Y, l_{\infty})$$. Dla ustalonych $$n, N \in \mathbb{N}$$, $$n < N$$ niech $$\lambda^N_n(Y) = \sup\{ \lambda(Y) : Y \subset l_{\infty}^{(N)},\, \dim(Y) = n\}$$. Podczas referatu przedstawię kilka rezultatów i otwartych problemów związanych z efektywnym wyznaczaniem $$n$$-wymiarowych przestrzeni $$Y\subset l_{\infty}^{(N)}$$ takich, że $$\lambda(Y, l_{\infty}^{(N)}) = \lambda^N_n$$.
to
> Niech $$X$$ będzie przestrzenią Banacha nad $$\mathbb{R}$$, a $$Y\subset X$$ jej podprzestrzenią domkniętą. Oznaczmy symbolem $$\mathcal{P}(X,Y)$$ wszystkie rzutowania liniowe i ciągłe z $$X$$ na $$Y$$. Niech $$\lambda(Y,X)=\inf\{\|P\|:P\in\mathcal{P}(X,Y)\}$$. Dla $$n$$-wymiarowej przestrzeni Banacha $$Y$$ niech $$\lambda(Y) = \sup \{ \lambda(Y,X): Y \subset X \}$$. Stała $$\lambda(Y)$$ nazywana jest w literaturze //absolutną stałą projekcji//. Jest znanym faktem, że dla $$n$$-wymiarowej przestrzeni Banacha $$Y$$, $$\lambda(Y) = \lambda(Y, l_{\infty})$$. Dla ustalonych $$n, N \in \mathbb{N}$$, $$n < N$$ niech $$\lambda^N_n(Y) = \sup\{ \lambda(Y) : Y \subset l_{\infty}^{(N)},\, \dim(Y) = n\}$$. Podczas referatu przedstawię kilka rezultatów i otwartych problemów związanych z efektywnym wyznaczaniem $$n$$-wymiarowych przestrzeni $$Y\subset l_{\infty}^{(N)}$$ takich, że $$\lambda(Y, l_{\infty}^{(N)}) = \lambda^N_n$$.
Wykład odbędzie się w piątek o 15.00 w sali B3-38
prof. dr hab. Grzegorz Lewicki (Instytut Matematyki Uniwersytetu Jagiellońskiego)
Przestrzenie z maksymalną stałą projekcji
Niech 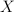 będzie przestrzenią Banacha nad
będzie przestrzenią Banacha nad 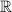 , a
, a 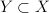 jej podprzestrzenią domkniętą. Oznaczmy symbolem
jej podprzestrzenią domkniętą. Oznaczmy symbolem 202424.png) wszystkie rzutowania liniowe i ciągłe z
wszystkie rzutowania liniowe i ciągłe z 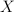 na
na 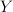 . Niech
. Niech 3d5cinf5c7b5c7cP5c7c3aP5cin5cmathcal7bP7d(X2cY)5c7d202424.png) . Dla
. Dla 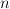 -wymiarowej przestrzeni Banacha
-wymiarowej przestrzeni Banacha 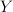 niech
niech 203d205csup205c7b205clambda(Y2cX)3a20Y205csubset20X205c7d202424.png) . Stała
. Stała 202424.png) nazywana jest w literaturze absolutną stałą projekcji. Jest znanym faktem, że dla
nazywana jest w literaturze absolutną stałą projekcji. Jest znanym faktem, że dla 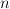 -wymiarowej przestrzeni Banacha
-wymiarowej przestrzeni Banacha 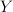 ,
, 203d205clambda(Y2c20l_7b5cinfty7d)202424.png) . Dla ustalonych
. Dla ustalonych 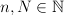 ,
, 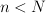 niech
niech 203d205csup5c7b205clambda(Y)203a20Y205csubset20l_7b5cinfty7d5e7b(N)7d2c5c2c205cdim(Y)203d20n5c7d202424.png) . Podczas referatu przedstawię kilka rezultatów i otwartych problemów związanych z efektywnym wyznaczaniem
. Podczas referatu przedstawię kilka rezultatów i otwartych problemów związanych z efektywnym wyznaczaniem 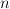 -wymiarowych przestrzeni
-wymiarowych przestrzeni 7d202424.png) takich, że
takich, że 7d)203d205clambda5eN_n202424.png) .
.