Last edit
Changed:
< {{{}}}**TITLE**
< ABSTRACT.
to
> {{{}}}**$$BV_{\phi}$$-solutions of nonlinear integral equations**
> In this talk we will deal with solutions of nonlinear Hammerstein and Volterra-Hammerstein integral equations in the space of functions of bounded $$\phi$$-variation in the sense of Young. We will discuss the existence and in some cases the existence and uniqueness of local and global solutions in this class. Real-valued as well as vector-valued functions will be under our consideration. The method of our proofs is based on an application of the Banach contraction principle as well as the Leray-Schauder alternative for contractions.
Daria Bugajewska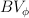
-solutions of nonlinear integral equations
In this talk we will deal with solutions of nonlinear Hammerstein and Volterra-Hammerstein integral equations in the space of functions of bounded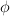 
-variation in the sense of Young. We will discuss the existence and in some cases the existence and uniqueness of local and global solutions in this class. Real-valued as well as vector-valued functions will be under our consideration. The method of our proofs is based on an application of the Banach contraction principle as well as the Leray-Schauder alternative for contractions.