Jacek Gulgowski
Rozwiązania o ograniczonym wahaniu zagadnień Sturma-Liouville'a
W ogólnej formie zagadnienia Sturm-Liouville'a postawić można w następujący sposób:
x5cprime20(t))5cprime202bq(t)x(t)3dh(t)5cquad205ctext7bdla20p.w.207d20t205cin20(02c1)2c5c5c0aa_0x(0)2bb_0x5cprime20(0)3d02c5c5c0aa_1x(1)2bb_1x205cprime20(1)3d02c0a5cend7bcases7d0a205cend7bdisplaymath7d.png) (1)
(1)gdzie
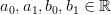 są odpowiednimi stałymi.
są odpowiednimi stałymi.Przy naturalnych założeniach obejmujących 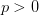 ,
, 202424.png) , otrzymujemy istnienie i jednoznaczność rozwiązań klasy
, otrzymujemy istnienie i jednoznaczność rozwiązań klasy ![$$ C^1[0,1] $$](http://octd.wmi.amu.edu.pl/latex/242420C5e15b02c15d202424.png) tego zagadnienia. Okazuje się jednak, że osłabiając założenia na funkcje $p$ oraz
tego zagadnienia. Okazuje się jednak, że osłabiając założenia na funkcje $p$ oraz 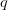 , uzyskać można w dalszym ciągu dobrze postawione zagadnienia (tzw. osobliwe zagadnienia Sturma-Liouville'a), dla których uzyskujemy istnienie rozwiązań z przestrzeni
, uzyskać można w dalszym ciągu dobrze postawione zagadnienia (tzw. osobliwe zagadnienia Sturma-Liouville'a), dla których uzyskujemy istnienie rozwiązań z przestrzeni 202424.png) . W tej sytuacji zasadne jest pytanie o to, czy uzyskane rozwiązania są funkcjami o ograniczonym wahaniu. Postaramy się podać warunki, przy których rozwiązania rozpatrywanego zagadnienia są funkcjami o ograniczonym wahaniu.
. W tej sytuacji zasadne jest pytanie o to, czy uzyskane rozwiązania są funkcjami o ograniczonym wahaniu. Postaramy się podać warunki, przy których rozwiązania rozpatrywanego zagadnienia są funkcjami o ograniczonym wahaniu.