Adam Nawrocki
Asymptotyczne zachowanie pewnych funkcji 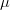 -prawie okresowych
-prawie okresowych
Funkcja
3d5cfrac7b17d7b22b5ccos20x202b5ccos7b(x5csqrt202)7d7d0a205cend7bdisplaymath7d.png) (4)
(4)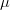 -prawie okresowej. Dla tej funkcji zachodzi
-prawie okresowej. Dla tej funkcji zachodzi7d7d3d0.0a205cend7bdisplaymath7d.png) (5)
(5)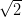 na inną liczbę niewymierną może znacząco wpłynąć na zachowanie funkcji. Skonstruujemy liczbę niewymierną
na inną liczbę niewymierną może znacząco wpłynąć na zachowanie funkcji. Skonstruujemy liczbę niewymierną 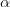 taką, że granica
taką, że granica7d7d0a205cend7bdisplaymath7d.png) (6)
(6)Referat zostanie poprzedzony krótkim komunikatem, który wygłosi Marcin Borkowski.