dr Piotr Maćkowiak
(Uniwersytet Ekonomiczny w Poznaniu)
O pewnej wersji twierdzenia o hiperpłaszczyźnie oddzielającej zbiory wypukłe
W literaturze dotyczącej optymalizacji i analizy wypukłej znany jest szereg definicji hiperpłaszczyzny oddzielającej zbiory wypukłe. Najbardziej znane (i być może najczęściej stosowane) jest twierdzenie o rozdzielaniu zbiorów wypukłych i domkniętych, z których przynajmniej jeden jest zwarty. Zaprezentujemy pewną wersje twierdzenia o rozdzielaniu pary zbiorów domkniętych i wypukłych, z których żaden nie musi być zwarty. Pokażemy, że twierdzenie jest prawdziwe dla przestrzeni co najwyżej dwuwymiarowych i wskażemy kontrprzykład dla przestrzeni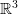 
. Ponadto - w miarę możliwości czasowych - podamy przykłady zbiorów dla których twierdzenie pozostaje prawdziwe oraz zastosowania przy dowodach tzw. twierdzeń o alternatywie.