Piotr Kasprzak
Application of the 202424.png)
cone to theory of multifunctions
We will discuss extension property for multifunctions. The Radström-Hörmander embedding theorem, which states that the cone consisting of all non-empty, closed, bounded and convex subset of a normed space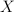 
can be isometrically and algebraically embedded as a convex cone in a Banach space, plays a key role in the proofs of the presented results. The talk is based on the paper Applications of the Radström-Hörmander Embedding Theorem to Multifunctions, Bull. Acad. Pol. Sci. Math. 53 (3) (2005), 259-271 by Anna Kucia.