On superposition operators in spaces of functions of bounded variations with applications to non-linear integral equations
In this talk we are going to present some sufficient conditions under which the classical superposition operator maps the space of functions of bounded variation into itself. We will consider the variation in the sense of Jordan, Young and also so-called generalized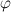 
-variation.
As applications of those results we are going to present some theorems on the existence and uniqueness of solutions to the non-linear Hammerstein as well as Volterra-Hammerstein integral equations. We will consider solutions to these equations (local as well as global) belonging to the space of functions of bounded variation in the above mentioned meanings.