Here are the titles and abstracts of the seminars which were held in 2014:
2014-12-09 Nonlinear Seminar
Monika Naskręcka
The existence of solutions of a certain system of differential equations with discontinuous right-hand side.
During this seminar we will discuss the existence of solutions of a certain system of differential equations with discontinuous right-hand side. This system depicts the dynamics of supplies in a model of competitive economy.
2014-12-02 Nonlinear Seminar
Marcin Borkowski
On a certain fixed point theorem for ultrametric spaces
We will discuss some variant of the Banach Contraction Principle, announced by N. Ackerman, for ultrametric spaces with metrics with values in a complete lattice.
(Continuation of the 2014-11-18 and 2014-11-04 Nonlinear Seminar.)
2014-11-25 Nonlinear Seminar
dr Przemysław Chełminiak
Stochastic dynamics of self-organizing critical nets
Self-organizing critical nets have been an object of intense research for over 15 years. They possess many peculiar properties, namely: fractality, self-similarity, topological criticality, little world effect and they are scale-free, which follow from their stochastic evolution. It occurs that many of such nets exist in an unstable state on the boundary of two phases, small-fractal world. Methods of construction and analysing critical nest will be shown, along with basic properties of probability distributions of stationary streams following stochastic dynamics of such nets.
2014-11-18 Nonlinear Seminar
Marcin Borkowski
On a certain fixed point theorem for ultrametric spaces
We will discuss some variant of the Banach Contraction Principle, announced by N. Ackerman, for ultrametric spaces with metrics with values in a complete lattice.
(Continuation of the 2014-11-04 Nonlinear Seminar.)
2014-11-04 Nonlinear Seminar
On a certain fixed point theorem for ultrametric spaces
We will discuss some variant of the Banach Contraction Principle, announced by N. Ackerman, for ultrametric spaces with metrics with values in a complete lattice.
2014-10-28 Nonlinear Seminar
Dr Mateusz Maciejewski
Existence of positive solutions of systems of parabolic equations with non-local initial conditions.
The topic of this speech is the existence of positive solutions of systems of parabolic equations with the boundary Dirichlet conditions and non-local initial conditions. For this purpose I shall show a fixed point theorem, which proof is based on Granas' fixed-point index. Thanks to the possibility of localisation of solutions I shall receive a theorem about existence of more than one solution.
2014-10-21 Nonlinear Seminar
Marcin Borkowski
Fixed point theorems with a boundary condition
2014-10-14 Nonlinear Seminar
Piotr Kasprzak
The game of Hex and the Brouwer fixed-point theorem.
During the seminar we are going to porve show that the celebrated Boruwer fixed-point theorem is a consequence of the fat that Hex cannot end in a draw.
2014-10-07 Nonlinear Seminar
Marcin Borkowski
Fixed point theorems with a boundary condition
In 1998, Espínola and López proved a certain fixed point theorem for a mapping transforming an admissible subset 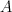 of a hyperconvex metric space into the whole space, assuming that this mapping sends the boundary of
of a hyperconvex metric space into the whole space, assuming that this mapping sends the boundary of 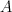 into
into 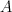 . We will show how to simplify their proof considerably, at the same time relaxing its assumptions. In particular, this will enable proving a new fixed point theorem, generalizing a classical result of Baillon from 1988.
. We will show how to simplify their proof considerably, at the same time relaxing its assumptions. In particular, this will enable proving a new fixed point theorem, generalizing a classical result of Baillon from 1988.
2014-09-30 Nonlinear Seminar
prof. Gennaro Infante
Nontrivial solutions of perturbed Hammerstein integral equations
We discuss the existence of positive solutions of some perturbed Hammerstein integral equations by means of classical fixed point index theory.We apply our results to some nonlocal BVPs that arise in some heat flow problems to prove the existence of multiple positive solutions under suitable conditions. We also illustrate how this approach might be applied to different problems.
2014-09-16 Nonlinear Seminar
Dariusz Bugajewski
BV-solutions of nonlinear equations
During the seminar we are going to prove the existence of BV-solutions to several nonlinear equations using the fixed point approach.
2014-06-10 Nonlinear Seminar
Adam Nawrocki
The convolution operator defined on the space of Levitan almost periodic functions.
(Continuation of the 2014-05-27 Nonlinear Seminar)
2014-05-27 Nonlinear Seminar
Adam Nawrocki
The convolution operator defined on the space of Levitan almost periodic functions.
It is known, that the convolution of a bounded, Levitan almost periodic function with a 202424.png) function is a bounded, Levitan almost periodic function. During this lecture we shall discuss the result we will receive when unbounded Levitan almost periodic functions are used.
function is a bounded, Levitan almost periodic function. During this lecture we shall discuss the result we will receive when unbounded Levitan almost periodic functions are used.
2014-05-20 Nonlinear Seminar
Adam Nawrocki
Asymptotic behaviour of a certain almost periodic function with regard to the Lebesgue measure
The function
3d5cfrac7b17d7b22b5ccos20x202b5ccos7b(x5csqrt202)7d7d0a205cend7bdisplaymath7d.png) (1)
(1)is a classical example of an unbounded and continuous
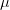 -almost periodic function. For this function we have
-almost periodic function. For this function we have7d7d3d0.0a205cend7bdisplaymath7d.png) (2)
(2)During this lecture we will discuss the idea of the proof of the equality above, which uses diophantic approximations. We shall furthermore show, that the limit
7d7d0a205cend7bdisplaymath7d.png) (3)
(3)does not exist.
2014-05-06 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2014-04-29, 2014-03-25, 2014-01-28, 2014-01-21, 2013-11-05 and 2013-10-29 Nonlinear Seminar)
2014-04-29 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2014-03-25, 2014-01-28, 2014-01-21, 2013-11-05
and 2013-10-29 Nonlinear Seminar)
2014-04-15 Nonlinear Seminar
Adam Nawrocki
Asymptotic behaviour of some 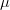 -almost periodic functions
-almost periodic functions
The function
3d5cfrac7b17d7b22b5ccos20x202b5ccos7b(x5csqrt202)7d7d0a205cend7bdisplaymath7d.png) (4)
(4)is a classical example of an unbounded and continuous
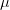 -almost periodic function. For this function we have
-almost periodic function. For this function we have7d7d3d0.0a205cend7bdisplaymath7d.png) (5)
(5)During this lecture we will consider if changing the number
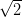 to another irrational number may have relevant impact on the behaviour of this function. We shall construct such a number
to another irrational number may have relevant impact on the behaviour of this function. We shall construct such a number 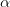 that the limit
that the limit7d7d0a205cend7bdisplaymath7d.png) (6)
(6)will not exist.
The lecture will be preceded by a short speech by Marcin Borkowski.
2014-04-01 Nonlinear Seminar
dr Michał Goliński
About some properties of the space of almost periodic functions
We will be talking about some properties of the space 202424.png) of the almost periodic functions, in particular the properties of the weak topology on this space (Cauchy sequences, completeness, reflexivity).
of the almost periodic functions, in particular the properties of the weak topology on this space (Cauchy sequences, completeness, reflexivity).
2014-03-25 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2013-10-29 and 2013-11-05 Nonlinear Seminar.)
2014-03-18 Nonlinear Seminar
Marcin Borkowski
On some application of Mönch theorem
(Continuation of the 2014-02-25 and 2014-03-04 Nonlinear Seminar.)
2014-03-11 Nonlinear Seminar
Dr Jacek Gulgowski
(Institute of Mathematics, Gdańsk University)
On the continuity of superposition operator in the spaces of functions of bounded variation
It is a well-know fact that the superposition of a function 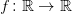 satisfying a local Lipschitz condition with a function
satisfying a local Lipschitz condition with a function 202424.png) of bounded variation leads to the function
of bounded variation leads to the function (t)202424.png) which is also of bounded variation. During the seminar we are going to present a few results concerning the continuity of such a superposition operator
which is also of bounded variation. During the seminar we are going to present a few results concerning the continuity of such a superposition operator ![$$ F \colon BV[0,1]\to BV[0,1] $$](https://octd.wmi.amu.edu.pl/latex/242420F205ccolon20BV5b02c15d5cto20BV5b02c15d202424.png) . Furthermore, we are going to discuss several generalizations of the concept of bounded variation in the sense of Jordan and investigate the issue of continuity of the superposition operator
. Furthermore, we are going to discuss several generalizations of the concept of bounded variation in the sense of Jordan and investigate the issue of continuity of the superposition operator ![$$ F \colon BV[0,1]\to E $$](https://octd.wmi.amu.edu.pl/latex/242420F205ccolon20BV5b02c15d5cto20E202424.png) , where
, where 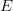 denotes the space of functions of bounded variation in the generalized sense.
denotes the space of functions of bounded variation in the generalized sense.
2014-03-04 Nonlinear Seminar
Marcin Borkowski
On some application of Mönch theorem.
(Continuation of the 2014-02-25 Nonlinear Seminar.)
2014-02-25 Nonlinear Seminar
Marcin Borkowski
On some application of Mönch theorem.
2014-01-28 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2014-01-21 Nonlinear Seminar)
2014-01-21 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2013-10-29 and 2013-11-05 Nonlinear Seminar)
2014-01-14 Nonlinear Seminar
prof. UW dr hab. Urszula Foryś (Warsaw University)
Modelling of biochemical reactions with delays
Nowadays, in the description of biochemical reactions not only ordinary differential equations but also equations with delays are applied. Time delays can be used to reflect different time scales at which modelled reactions occur. During our (together with M. Bodnarem, J. Miękisz and J. Poleszczuk) research we have found that simple, intuitive methods of introducing delay can lead to improper conclusions, such as oscillatory dynamics of the simple protein delayed degradation process. I shall show that the simplest model proposed by Bartsun et al. (2005) should be modified. It occurs that to obtain oscillatory dynamics one needs to consider much more complex reactions channel, with negative feedback and dimerization.
The seminar is to be held in room B1-37.
2014-01-07 Nonlinear Seminar
dr Aneta Sikorska-Nowak
Nonlinear Sturm – Liouville dynamic equation
Will be presented the necessary concepts of dynamic equations on time scales, and nonlinear dynamic equation of Sturm-Liouville.