Here are the titles and abstracts of the seminars which were held in 2012:
2012-12-18 Nonlinear Seminar
Monika Naskręcka
Homeomorphism of the space of polynomials and the space of their roots
(Continuation of the 2012-12-11 Nonlinear Seminar)
2012-12-11 Nonlinear Seminar
Monika Naskręcka
Homeomorphism of the space of polynomials and the space of their roots
During this seminar an elementary, topological proof of continuity of the roots of complex polynomials with respect to their roots will be shown. For normed polynomials with complex coefficients and properly defined metric spaces this theorem can be expressed as a homeomorphism of corresponding metric spaces of coeffecients and roots.
2012-12-04 Nonlinear Seminar
Piotr Maćkowiak
The existence of surplus demand function zeros
(Continuation of the 2012-10-09 and 2012-10-16 Nonlinear Seminars.)
2012-11-27 Nonlinear Seminar
Piotr Zdanowicz
Basic properties of formal series
(Continuation of the 2012-11-20 Nonlinear Seminar)
2012-11-20 Nonlinear Seminar
Piotr Zdanowicz
Basic properties of formal series
2012-11-13 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of 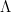 -bounded variation
-bounded variation
(Continuation of the 2012-10-30 Nonlinear Seminar)
2012-11-06 Nonlinear Seminar
The seminar will take place at 8:30 in the Faculty Council meeting room (A1-33/34)
Justyna Signerska
Firing map for integrate-and-fire models with an almost periodic drive
Consider the integrate-and-fire system 202424.png) ,
, 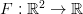 , in which the continuous dynamics is interrupted by the threshold-and-reset behaviour:
, in which the continuous dynamics is interrupted by the threshold-and-reset behaviour: 3dx_r202424.png) if
if 3dx_7b5cTheta7d202424.png) , meaning that once the value of a dynamical variable reaches a certain threshold
, meaning that once the value of a dynamical variable reaches a certain threshold 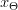 it is immediately reset to a resting value
it is immediately reset to a resting value 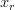 and the system evolves again according to the differential equation. The question is to describe the time series of consecutive resets (spikes)
and the system evolves again according to the differential equation. The question is to describe the time series of consecutive resets (spikes) 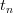 as iterations
as iterations 202424.png) of some map
of some map 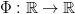 , called the firing map, and the sequence of interspike-intervals
, called the firing map, and the sequence of interspike-intervals 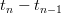 as a sequence of displacements
as a sequence of displacements -5cPhi5e7bn-17d(t_0)202424.png) along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.
along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.
However, so far properties of the firing map were analytically investigated only for the function 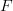 , which is smooth enough and often also periodic in
, which is smooth enough and often also periodic in 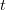 . We present a complete description of the properties of the firing map arising from the most popular models:
. We present a complete description of the properties of the firing map arising from the most popular models: 202424.png) (Leaky Integrate-and-Fire) and
(Leaky Integrate-and-Fire) and 202424.png) (Perfect Integrator), when the function
(Perfect Integrator), when the function  is only locally integrable and/or almost periodic. In particular, we prove that a Stepanov almost periodic function
is only locally integrable and/or almost periodic. In particular, we prove that a Stepanov almost periodic function  induces the firing map
induces the firing map 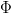 with the uniformly (Bohr) almost periodic displacement
with the uniformly (Bohr) almost periodic displacement 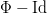 . In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.
. In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.
2012-10-30 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of 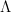 -bounded variation
-bounded variation
During the seminar we are going to define a certain class of functions of 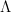 -bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
-bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
2012-10-23 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of 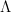 -bounded variation
-bounded variation
During the seminar we are going to define a certain class of functions of 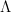 -bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
-bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
2012-10-16 Nonlinear Seminar
Piotr Maćkowiak
The existence of surplus demand function zeros
(Continuation of the 2012-10-09 Nonlinear Seminar)
2012-10-09 Nonlinear Seminar
Piotr Maćkowiak
The existence of surplus demand function zeros
2012-05-29 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of bounded variation
(Continuation of the 2012-04-24 Nonlinear Seminar)
2012-05-22 Nonlinear Seminar
Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
(Continuation of the 2012-05-08 Nonlinear Seminar)
2012-05-15 Nonlinear Seminar
Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
(Continuation of the 2012-05-08 Nonlinear Seminar)
2012-05-08 Nonlinear Seminar
Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
Arrow's impossibility theorem states, that if there are at least three potential social states, there is no such social welfare function  (that describes the society as a whole with given individual preferences), which satisfies the following four conditions:
(that describes the society as a whole with given individual preferences), which satisfies the following four conditions:  has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle;
has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle;  satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function
satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function  there is no dictatorship. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.
there is no dictatorship. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.
2012-04-24 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of bounded variation
We are going to define a relatively large class of functions of bounded variation defined on an open subset of 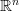 , which in particular contains the Sobolev space
, which in particular contains the Sobolev space 202424.png) . Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.
. Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.
2012-04-03 Nonlinear Seminar
Piotr Kasprzak
On the compactness criterion in the space of bounded real-valued continuous functions defined on a non-compact domain
During the seminar we are going to discuss a certain compactness criterion in the space of bounded real-valued continuous functions defined on a non-compact domain related to the well-known Arzela-Ascoli theorem.
2012-03-27 Nonlinear Seminar
Piotr Maćkowiak
Exploding points
We will present and prove theorem of the exploding point. This theorem states that for any function defined on a compact set X, containing the cube K centered at zero in its interior, with values in X\K, which is the identity on the boundary of the set X, there exists a point c in X, that in any surroundings of c, there is a point x such that the value of f(x) and f(c) are located on opposite walls of the cube K.
2012-03-20 Nonlinear Seminar
Adam Nawrocki
An Application of Continued Fractions
During this seminar we will discuss basic properties of Continued Fractions. Next we shall use Continued Fractions to calculate the limit of:2b5ccos(5csqrt7b27dx)7d202424.png)
(Continuation of the 2012-03-13 Nonlinear Seminar)
2012-03-13 Nonlinear Seminar
Adam Nawrocki
An Application of Continued Fractions
During this seminar we will discuss basic properties of Continued Fractions. Next we shall use Continued Fractions to calculate the limit of:2b5ccos(5csqrt7b27dx)7d202424.png)
2012-03-06 Nonlinear Seminar
Marcin Wachowiak
Applications of Theorem Hopf-Lefschetz fixed point
(Continuation of the 2011-11-22 Nonlinear Seminar and 2011-11-29 Nonlinear Seminar and 2011-12-06 Nonlinear Seminar).
2012-02-28 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar, 2012-01-03 Nonlinear Seminar, 2012-02-14 Nonlinear Seminar and 2012-02-21 Nonlinear Seminar).
2012-02-21 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar and 2012-01-03 Nonlinear Seminar and 2012-02-14 Nonlinear Seminar).
2012-02-14 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar and 2012-01-03 Nonlinear Seminar).
2012-01-24 Nonlinear Seminar
Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
(Continuation of the 2012-01-10 Nonlinear Seminar and 2012-01-17 Nonlinear Seminar).
2012-01-17 Nonlinear Seminar
Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
(Continuation of the 2012-01-10 Nonlinear Seminar).
2012-01-10 Nonlinear Seminar
Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
We are going to consider linear differential and nonlinear integral equations in the
spaces of functions of Lambda-bounded variation. We will state the existence and the existence and uniqueness results in this space as well as in its subspace consisting of contninuous functions of Lambda-bounded variation.
2012-01-03 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar).