The Nonlinear seminar of the OCTD is held on Tuesdays at 10:00 am in room B3-49, in the Faculty building in Umultowska street 87 in Poznań.
The seminar is conducted by prof. UAM dr hab. Dariusz Bugajewski.
Next seminar
Topics discussed
The seminar is devoted to discussing problems in nonlinear analysis. Instead of presenting known results, we prefer to discuss open problems connected with the current research of the seminar members.
We pay particular attention to the following topics.
- Fixed point theorems for different classes of mappings acting in linear vector spaces, hyperconvex metric spaces or absolute retracts.
- Almost periodic and almost automorphic functions and their generalizations and applications to differential and integral equations.
- Functions of bounded variation with applications to the theory of nonlinear integral and superposition operators.
- Existence and uniqueness of solutions to nonlinear integral equations in spaces of functions of bounded variation (in various senses).
- Existence and topological structure of solutions sets of nonlinear differential and integral equations in finite-dimensional and abstract spaces.
- Selected topics from general topology: measures of noncompactness, hyperconvex spaces, R-trees and others.
- Selected topics in the theory of nonabsolute convergent integrals.
- Selected problems of formal analysis.
Seminar archive
Here are the titles and abstracts of the seminars:
2019-01-08 Nonlinear Seminar
Jin Haixia
The Aleksandrov problem in non-Archimedean 2-fuzzy 2-normed space
We will introduce the concept of isometry which is suitable to represent the notion of area preserving mapping in non-Archimedean 2-fuzzy 2-normed space. Then we obtain some results by applying the Ben's theorem for the Aleksandrow problem in non-Archimedean 2-fuzzy 2-normed space.
2018-12-18 Nonlinear Seminar
Shunxin Zhao
Wigner’s theorem in s space
Wigner theorem is the cornerstone of the mathematical formula of quantum mechanics, it has promoted the research of basic theory of quantum mechanics. In this talk, we give a certain pair of functional equations between two real spaces s, that we called “phase isometry”. It is obtained that all such solutions are phase equivalent to real linear isometries in the space s.
2018-12-11 Nonlinear Seminar
Zhongqin Gao
Omega model for a jump-diffusion process with a two-step premium rate
In this talk, a jump-diffusion Omega model with a two-step premium rate is studied. In this model, the surplus process is a perturbation of a compound Poisson process by a Brown motion. Firstly, using the strong Markov property and Taylor formula, the integro-differential equations for the Gerber-Shiu expected discounted penalty function and the bankruptcy probability are derived. Secondly, for a constant bankruptcy rate function, the renewal equations satisfied by the Gerber-Shiu expected discounted penalty function are obtained, and by iteration, the closed-form solutions of the function are also given. Further, the explicit solutions of the Gerber-Shiu expected discounted penalty function are obtained when the individual claim size is subject to exponential distribution. Finally, a numerical example is presented to illustrate some properties of the model.
2018-12-04 Nonlinear Seminar
Xihong Jin
(Tianjin University of Technology, Tianjin, China)
A variety of Tingley problem in 202424.png) -spaces
-spaces
During the seminar we are going to prove that for every surjective phaseisometry between the unit spheres of real 202424.png) -type spaces, its positive homogeneous extension is a phase-isometry which is phase-equivalent to a linear isometry.
-type spaces, its positive homogeneous extension is a phase-isometry which is phase-equivalent to a linear isometry.
The seminar starts at 12:45.
2018-11-27 Nonlinear Seminar
Michał Wojtal
Existence of square-mean almost periodic solutions to some stochastic differential equations
We will present certain class of stochastic hyperbolic differential equations with infinite delay. Next, we show existence of square-mean almost periodic solutions to equations of this type using Krasnoselskii's Fixed Point Theorem. Presentation is based on paper "Existence of square-mean almost periodic solutions to some stochastic hyperbolic differential equations with infinite delay" by P. Bezandry and T. Diagana.
2018-11-20 Nonlinear Seminar
Adam Nawrocki
Autonomous superposition operator defined on the space of generalized almost periodic functions
(Continuation of the 2018-11-13 Nonlinear Seminar)
2018-11-13 Nonlinear Seminar
Adam Nawrocki
Autonomous superposition operator defined on the space of generalized almost periodic functions
During the seminar we consider the autonomous superposition operator defined on the space of almost periodic functions in view of the Lebesgue measure. In particular, we give connection of this class with the class of the Stepanov almost periodic functions.
2018-11-06 Nonlinear Seminar
Adam Nawrocki
Some remarks concerning the convolution of a certain almost periodic function
(Continuation of the 2018-10-23 Nonlinear Seminar)
2018-10-30 Nonlinear Seminar
Adam Nawrocki
Some remarks concerning the convolution of a certain almost periodic function
(Continuation of the 2018-10-23 Nonlinear Seminar)
The seminar has been canceled and is rescheduled for Tuesday, November 6, 2018.
2018-10-23 Nonlinear Seminar
Adam Nawrocki
Some remarks concerning the convolution of a certain almost periodic function
For 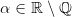 we define the family of the functions
we define the family of the functions3d5cfrac7b17d7b22b5ccos20x202b5ccos(5calpha20x)7d202424.png) dla
dla 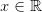 .
.
Moreover for 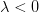 let
let 3de5e7b5clambda20x7d202424.png) if
if 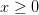 and
and 3d0202424.png) if
if 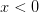 . Then the sets
. Then the sets 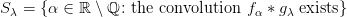 and
and 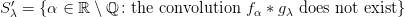 are dense subsets of
are dense subsets of 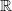 . During the seminar we give properties of these sets from the point of view of set theory, measure theory and topology.
. During the seminar we give properties of these sets from the point of view of set theory, measure theory and topology.
The seminar starts at 10:45.
2018-10-16 Nonlinear Seminar
Kosma Kasprzak
About calculating certain limits
(Continuation of the 2018-10-09 Nonlinear Seminar)
2018-10-09 Nonlinear Seminar
Kosma Kasprzak
About calculating certain limits
In the first part of the talk we will show two ways of calculating the following limit: 7d202424.png) . In the second part we are going to present some extensions of that result as well as other results connected with this limit.
. In the second part we are going to present some extensions of that result as well as other results connected with this limit.
2018-10-02 Nonlinear Seminar
Simon Reinwand (Uniwersitet w Würzburgu)
On some Disparities of Multiplication and Composition Operators in BV Spaces
Although multiplication and composition of two functions are first grade operations, the corresponding multiplication and (autonomous) composition operator exhibit many weird and difficult to handle properties in BV spaces. We give criteria for acting conditions, as well as for injectivity, surjectivity, bijectivity and compactness in BV spaces. This leads naturally to a comprehensive study of multiplier sets, of which we will give a short overview. While most of them are easy to determine, some of them - especially those related to classical functions like Darboux and continuous functions - are unknown to our knowledge.
Moreover, we introduce a new type of convergence for composition operators in BV which leads to new a new proof for old continuity criteria. We hope that those ideas can be generalized to other BV-type spaces and give the relevant ideas and conjectures.
Apart from recalling known and discussing new results we put a particular emphasis on examples and counter examples.
2018-06-19 Nonlinear Seminar
Ruidong Wang
The Tingley's Problem on two dimensional normed spaces
(Continuation of the 2018-06-12 Nonlinear Seminar)
2018-06-12 Nonlinear Seminar
Ruidong Wang
The Tingley's Problem on two dimensional normed spaces
In this seminar I will talk about the metric properties of the unit sphere of a two dimensional normed space and the Tingley's problem on two dimensional normed spaces.
2018-06-05 Nonlinear Seminar
dr Jacek Gulgowski (Gdańsk University)
Integral variation and piecewise polynomial approximation
The concept of integral variation appears to be related to some problems considered in the approximation theory. The concept of polynomials of best approximation leads to certain norm that is equivalent to the q-integral p-variation norm.
2018-05-29 Nonlinear Seminar
Xiao-Xiong Gan (Morgan State University, Baltimore MD, USA)
From Formal Power Series to Formal Analysis
For any 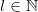 , a formal power series on a ring
, a formal power series on a ring  is defined to be a mapping from
is defined to be a mapping from  to
to  . A formal power series
. A formal power series  in
in  from
from 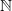 to
to 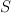 is usually denoted as a sequence
is usually denoted as a sequence 202424.png) or as a power series
or as a power series 203d20a_0202b20a_120z202b205ccdots202b20a_n20z5en202b205ccdots202424.png) , where
, where 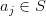 for every
for every 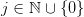 . The set of all formal power series on
. The set of all formal power series on 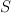 is denoted by
is denoted by 202424.png) .
.
If considering a formal power series as a sequence, what is the difference between 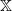 and
and 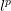 ?
?
If considering a formal power series as a power series, what is the difference between formal power series and the traditional power series? What is the relationship between formal power series and traditional power series?
What is formal analysis?
This talk tries to answer those questions and brings discussion of all kinds of questions about formal analysis, a relatively new mathematical subject.
2018-05-08 Nonlinear Seminar
Michał Wojtal
Introduction to stochastic integral
(Continuation of the seminars from 2018-01-16, 2018-01-30, 2018-02-27 and 2018-03-27)
2018-04-24 Nonlinear Seminar
Ruidong Wang
On isometric extension problem on the unit sphere of normed spaces
(Continuation of the 2018-04-10 and 2018-04-17 seminars)
2018-04-17 Nonlinear Seminar
Ruidong Wang
On isometric extension problem on the unit sphere of normed spaces
(Continuation of the 2018-04-10 Nonlinear Seminar)
2018-04-10 Nonlinear Seminar
Ruidong Wang
On isometric extension problem on the unit sphere of normed spaces
The isometric extension problem has been studied by a number of mathematicians, and there are many deep and interesting partial results, even this problem has not been solved till now.
2018-03-27 Nonlinear Seminar
Michał Wojtal
Introduction to stochastic integral
(Continuation of the seminars from 2018-01-16, 2018-01-30 and 2018-02-27)
2018-03-13 Nonlinear Seminar
Marcin Borkowski
On partial metric spaces
(Continuation of the 2017-11-28 and 2018-03-06 seminars)
2018-03-06 Nonlinear Seminar
Marcin Borkowski
On partial metric spaces
(Continuation of the 2017-11-28 Nonlinear Seminar)
2018-02-27 Nonlinear Seminar
Michał Wojtal
Introduction to stochastic integral
(Continuation of the seminars from 2018-01-16 and 2018-01-30)
2018-01-30 Nonlinear Seminar
Michał Wojtal
Introduction to stochastic integral
(Continuation of the 2018-01-16)
2018-01-16 Nonlinear Seminar
Michał Wojtal
Introduction to stochastic integral
During the talk we will discuss the construction of stochastic integral and it's basic properties.
2018-01-09 Nonlinear Seminar
Piotr Kasprzak
On a certain fixed point theorem in Banach algebras
During the seminar we are going to discuss a certain version of the Krasnoselskii fixed point theorem for the sum of two operators in Banach algebras.
2018-01-05 Nonlinear Seminar
Jian Meng (Tianjin University of Technology, China)
On some binomial difference sequence spaces
The matrix domains of Cesàro mean, Riesz mean 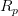 , Nörlund mean
, Nörlund mean 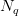 and Euler mean of order r in the sequence spaces
and Euler mean of order r in the sequence spaces 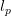 ,
, 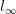 , c and
, c and 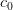 have been studied by some authors. The Binomial mean is one of the most important methods in the summability theory, but the matrix domain of binomial mean has not been studied, until now. The aim of this talk is to introduce the binomial difference sequence spaces. We prove some basic properties of these spaces and some inclusion relations. Moreover, we obtain the Schauder bases of some of these spaces and compute the α-, β- and γ-duals of these sequence spaces.
have been studied by some authors. The Binomial mean is one of the most important methods in the summability theory, but the matrix domain of binomial mean has not been studied, until now. The aim of this talk is to introduce the binomial difference sequence spaces. We prove some basic properties of these spaces and some inclusion relations. Moreover, we obtain the Schauder bases of some of these spaces and compute the α-, β- and γ-duals of these sequence spaces.
2017-12-19 Nonlinear Seminar
dr Jacek Gulgowski
Continuity of nonautonomous superposition operator in Lambda BV spaces
We are going to present sufficient conditions for the continuity of the nonautonomous superposition operator acting in Lambda BV spaces. The conditions cover generators of class 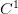 in two variables, but allow also for much broader class of functions.
in two variables, but allow also for much broader class of functions.
2017-11-28 Nonlinear Seminar
Marcin Borkowski
On partial metric spaces
The talk will be devoted to basic properties of so-called partial metric spaces and to proving a variant of the Banach contraction principle for such spaces. The talk is based on a paper /Parrtial metric topology/ by S. G. Matthews.
2017-11-21 Nonlinear Seminar
Piotr Kasprzak
On weak topology in the space ![$$ BV[0,1] $$](http://octd.wmi.amu.edu.pl/latex/24242020BV5b02c15d20202424.png)
The aim of the seminar is to present a characterization of the weak convergence in the space of functions of bounded Jordan variation. We are also going to discuss the weak compactness in such spaces.
(Continuation of the 2017-06-06 Nonlinear Seminar).
2017-10-17 Nonlinear Seminar
Piotr Kasprzak
On weak topology in the space ![$$ BV[0,1] $$](http://octd.wmi.amu.edu.pl/latex/24242020BV5b02c15d20202424.png)
The aim of the seminar is to present a characterization of the weak convergence in the space of functions of bounded Jordan variation. We are also going to discuss the weak compactness in such spaces.
(Continuation of the 2017-06-06 Nonlinear Seminar).
2017-10-10 Nonlinear Seminar
Simon Reinwand (University of Würzburg)
On Functions with Primitives
The problem of characterizing those functions, which possess a classical primitive has been investigated for decades. As far as we know, it is still an open problem if there is a “natural” characterization without involving integrals.
In this talk we give a quick overview about different characterizations while keeping our focus on probably the most natural one involving the Henstock-Kurzweil Integration Theory. While being a slight generalization of the Riemann Integral, it provides not only the most comprehensive version of the classical Fundamental Theorem of Calculus, but also yields a full characterization of the class of functions, which have a primitive.
We will discuss this class in more detail with respect to its size, its relation to other function classes, and some of its algebraic properties. Apart from recalling known and discussing new results we put a particular emphasis on examples and counter examples.
While answering questions regarding multiplication and change of variables we will point out connections between functions with primitives, Darboux-functions, HK-integrable functions and functions of bounded variation.
2017-06-06 Nonlinear Seminar
Piotr Kasprzak
On weak topology in the space ![$$ BV[0,1] $$](http://octd.wmi.amu.edu.pl/latex/242420BV5b02c15d202424.png)
The aim of the seminar is to present a characterization of the weak convergence in the space of functions of bounded Jordan variation. We are also going to discuss the weak compactness in such spaces.
2017-05-16 Nonlinear Seminar
Marcin Borkowski
On 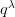 -hyperconvex quasi-metric spaces
-hyperconvex quasi-metric spaces
(Continuation of the seminars from 2017-04-04, 2017-04-11 and 2017-05-09)
2017-05-09 Nonlinear Seminar
Marcin Borkowski
On 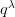 -hyperconvex quasi-metric spaces
-hyperconvex quasi-metric spaces
(Continuation of the seminars from 2017-04-04 and 2017-04-11)
2017-04-11 Nonlinear Seminar
Marcin Borkowski
On 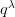 -hyperconvex quasi-metric spaces
-hyperconvex quasi-metric spaces
(Continuation of the seminar from 2017-04-04)
2017-04-04 Nonlinear Seminar
Marcin Borkowski
On 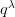 -hyperconvex quasi-metric spaces
-hyperconvex quasi-metric spaces
The aim of the talk is to introduce the definition and basic properties
of quasi-metric spaces and the notion of 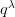 -hyperconvexity in
-hyperconvexity in
these spaces.
2017-03-21 Nonlinear Seminar
Marcin Borkowski
On some metric spaces
(Continuation of the seminars from 2016-10-04, 2016-10-11 and 2017-02-28)
2017-03-14 Nonlinear Seminar
Michał Goliński
Formal power series (Part 1)
(Continuation of the 2017-03-07)
2017-03-07 Nonlinear Seminar
Michał Goliński
Formal power series (Part 1)
At the seminar we will discuss the following statement of M. Artin:
Let 3d0202424.png) be analytic equation (
be analytic equation ( is analytic). We will show that if the equation has a solution
is analytic). We will show that if the equation has a solution 202424.png) in the space of formal series than it has also analytic solution which differs from
in the space of formal series than it has also analytic solution which differs from 20202424.png) coefficients with large powers.
coefficients with large powers.
2017-02-28 Nonlinear Seminar
Marcin Borkowski
On some metric spaces
(Continuation of the seminars from 2016-10-04 and 2016-10-11)
2017-01-31 Nonlinear Seminar
Piotr Maćkowiak
Action and continuity of superposition operators
(Continuation of the 2017-01-24)
2017-01-24 Nonlinear Seminar
Piotr Maćkowiak
Action and continuity of superposition operators
(Continuation of the 2016-11-15)
2017-01-17 Nonlinear Seminar
Marcin Borkowski
On some measures of efficiency of financial projects
(Continuation of the 2017-01-03)
2017-01-10 Nonlinear Seminar
Meng Liu
On the Generalized Hyers-Ulam-Rassias Stability of an k-Dimensional Quadratic Functional Equation
In this lecture, we investigate the generalized Hyers-Ulam-Rassias stability of an k- dimensional quadratic functional equation. At the same time, we will generalize the theorem of Jae-Hyeong Bae and Kil-Woung Jun. We also get Hyers-Ulam-Rassias stability of the k-dimensional quadratic functional equation in restricted domains.
2017-01-03 Nonlinear Seminar
Marcin Borkowski
On some measures of efficiency of financial projects
(Continuation of the 2016-12-13)
2016-12-20 Nonlinear Seminar
Meng Liu
Generalized stability of an AQ-functional equation in
quasi-(2;p)-Banach spaces
The stability of functional equation is a vital subject of functional
analysis. We introduce and investigate the general solution of a new
functional equation -AQ functional equation and discuss its Generalized
Hyers-Ulam-Rassias stability under the conditions such as even, odd,
approximately even and approximately odd in quasi-(2;p)-Banach spaces.
2016-12-13 Nonlinear Seminar
Marcin Borkowski
On some measures of efficiency of financial projects
A classic – and the most well-known – measure of efficiency of financial
projects is the net present value (NPV). However, it has certain issues
connected with choosing the “right” discount rate. In the paper by
Teichroew et al. (1965) it was shown how to compute net future value
using two rates: one for financing and one for reinvesting. The authors
mention how to use their method to compute an analogue of the NPV.
Unfortunately, their method is wrong. The first part of the talk will
be devoted to showing their error and comparing their method to
a correct one due to A. Kulakova (2010). Then, we will prove a number
of properties of the generalized net present value defined by the latter
author.
2016-12-06 Nonlinear Seminar
dr Giselle Monteiro
(Slovak Academy of Sciences)
Extremal solutions for measure differential equations
We investigate the existence of greatest and least solutions for the so-called measure differential equations - namely, integral equations in which the Stieltjes type integral is in the sense of Kurzweil. Based on these results, we derive new theorems about extremal solutions for impulsive systems.
Acknowledgement: Research financed by the SASPRO Programme, co-financed by the European Union and the Slovak Academy of Sciences.
2016-11-29 Nonlinear Seminar
dr Jacek Gulgowski
On functions of bounded 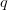 -integral
-integral 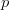 -variation
-variation
During the seminar we are going to discuss functions of bounded 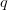 -integral
-integral 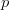 -variation. In particular, we are going to present some of their basic properties. We are also going to discuss the relationship of the space of such functions with Sobolev spaces. Finally, we are going to show some results on superposition operator and nonlinear integral operator acting in the space of functions of bounded
-variation. In particular, we are going to present some of their basic properties. We are also going to discuss the relationship of the space of such functions with Sobolev spaces. Finally, we are going to show some results on superposition operator and nonlinear integral operator acting in the space of functions of bounded 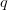 -integral
-integral 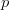 -variation.
-variation.
2016-11-15 Nonlinear Seminar
Piotr Maćkowiak
Action and continuity of superposition operators
During the seminar we will present results from the book R.M. Dudley, R. Norvaisa, Concrete functional calculus (Springer 2011) concerning conditions for the action and continuity of superposition operators acting in the space of functions of bounded variation in the Jordan sense.
2016-11-08 Nonlinear Seminar
Monika Naskręcka
Necessary and sufficient conditions of stability some particular differential equations system
(Continuation of the 2016-10-25)
2016-10-25 Nonlinear Seminar
Monika Naskręcka
Necessary and sufficient conditions of stability some particular differential equations system
(Continuation of the 2016-10-18)
2016-10-18 Nonlinear Seminar
Monika Naskręcka
Necessary and sufficient conditions of stability some particular differential equations system
During this seminar we will present lemmas and theorems which are necessary and sufficient conditions of stability some particular differential equations system with discontinuous right-hand side, which describe the dynamics of prices and stocks.
2016-10-04 Nonlinear Seminar
Marcin Borkowski
On some metric spaces
During the talk we will present certain construction of metric spaces,
described by Száz and generalizing the linking construction known
from Aksoy and Maurizi's paper. We will then proceed to examine some of
its properties, in particular connected with measures of noncompactness.
2016-06-14 Nonlinear Seminar
Marcin Borkowski
On hyperconvex hull of diversities
(Continuation of the 2016-06-07)
2016-06-07 Nonlinear Seminar
Marcin Borkowski
On hyperconvex hull of diversities
The talk will be devoted to problems with introducing the analogue of
hyperconvex hull (equivalently, tight span) of a diversity.
2016-05-31 Nonlinear Seminar
Lech Pasicki
Classical fixed point theorems
Author’s extensions of the well-known fixed point theorems will be presented. The theorem of Banach, the theorem of Caristi (also with the variational results), and the theorem of Browder-Göhde-Kirk for nonexpansive mappings are involved. Our versions extend these theorems, as their specific assumptions are weaker, and the spaces under consideration are more general.
2016-04-26 Nonlinear Seminar
Adam Nawrocki
Levitan almost periodic solutions to some linear differential equation
(Continuation of the 2016-04-19)
2016-04-19 Nonlinear Seminar
Adam Nawrocki
Levitan almost periodic solutions to some linear differential equation
During this lecture we will show that a Levitan almost periodic (briefly: LAP) solution to the equation 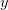 '
'3d5clambda20y(x)2bf(x)202424.png) usually can be expressed by means of convolution. We will show that in this way we can get an unbounded LAP solution. We will give an example showing that the convolution in not always a good tool to look for LAP solutions.
usually can be expressed by means of convolution. We will show that in this way we can get an unbounded LAP solution. We will give an example showing that the convolution in not always a good tool to look for LAP solutions.
2016-04-12 Nonlinear Seminar
Marcin Borkowski
Another look at hyperconvex hulls
The talk will be devoted to a certain generalization of the notion of
a metric space, inspired by applications to taxonomy, in which one can
introsuce an analogue of the notion of hyperconvexity. We will start
with an a bit atypical angle on Isbell's hyperconvex hull, and then we
will proceed to describe some problems with transferring his ideas to
the generalization in question.
2016-04-05 Nonlinear Seminar
Albert Kubzdela
On some properties of some measure of non-compactness in non-Archimedean analysis
Let 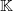 be a locally compact non-Archimedean field, and
be a locally compact non-Archimedean field, and 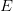 a non-Archimedean Banach space over
a non-Archimedean Banach space over 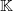 . We define non-Archimedean equivalents of several well-known measures of non-compactness defined on
. We define non-Archimedean equivalents of several well-known measures of non-compactness defined on 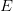 , we describe their properties and we present quantitative versions of several classic statements on weak compactness (theorems of Krein, Gantmacher and Grothendieck) for non-Archimedean Banach spaces.
, we describe their properties and we present quantitative versions of several classic statements on weak compactness (theorems of Krein, Gantmacher and Grothendieck) for non-Archimedean Banach spaces.
2016-03-22 Nonlinear Seminar
Adam Nawrocki
The autonomous superposition operator defined on the space of almost periodic functions in view of the Lebesgue measure
(Continuation of the 2016-03-15)
2016-03-15 Nonlinear Seminar
Adam Nawrocki
The autonomous superposition operator defined on the space of almost periodic functions in view of the Lebesgue measure
During this lecture we shall discuss autonomuous superposition operators generated by mappings 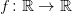 and acting in the space of
and acting in the space of 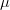 -almost periodic functions.
-almost periodic functions.
2016-03-08 Nonlinear Seminar
Piotr Maćkowiak
Continuity of the non-autonomous superposition operator and around
(Continuation of the 2016-01-26 and 2016-03-01 Nonlinear Seminar)
2016-03-01 Nonlinear Seminar
Piotr Maćkowiak
Continuity of the non-autonomous superposition operator and around
(Continuation of the 2016-01-26)
2016-01-26 Nonlinear Seminar
Piotr Maćkowiak
Continuity of the non-autonomous superposition operator and around
We shall present an example of a function ![$$ f:[0,1]\times\mathbb R\to \mathbb R $$](https://octd.wmi.amu.edu.pl/latex/242420f3a5b02c15d5ctimes5cmathbb20R5cto205cmathbb20R202424.png) which is lipschitzian and such that the (non-autonomous) superposition operator it generates is not continuous (as a mapping from
which is lipschitzian and such that the (non-autonomous) superposition operator it generates is not continuous (as a mapping from 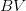 to
to 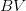 ). We shall show necessary and sufficient conditions for a non-autonomous superposition operator to be continuous (in
). We shall show necessary and sufficient conditions for a non-autonomous superposition operator to be continuous (in 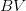 ). We shall also prove some results for
). We shall also prove some results for 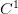 -class generators.
-class generators.
2016-01-19 Nonlinear Seminar
Marcin Borkowski
On some fixed point theorem in ultrametric spaces
(Continuation of the 2015-12-15 and 2016-01-12 Nonlinear Seminar)
2016-01-12 Nonlinear Seminar
Marcin Borkowski
On some fixed point theorem in ultrametric spaces
(Continuation of the 2015-12-15 Nonlinear Seminar)
2015-12-15 Nonlinear Seminar
Marcin Borkowski
On some fixed point theorem in ultrametric spaces
We will discuss a theorem establishing the existence of a fixed point and a (generalized) sequence approximating this fixed point. The talk is based in a paper by S. Priess-Crampe and P. Ribenboim from 2013.
2015-12-08 Nonlinear Seminar
Mateusz Krukowski
Darbo type theorem for quasi-measures of non-compactness.
This presentation introduces the notion of a quasi-measure of non-compactness. Such functions need not to be invariant in a convex hull in contrast to classical measures of non-compactness. Using the compactness criterion in the space 202424.png) (
(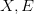 are Banach spaces with
are Banach spaces with 203c205cinfty202424.png) ), we construct a quasi-measure of non-compactness and study its properties. Furthermore we prove the analog of the Darbo theorem using the measure of non-convexity. We also show the application of the shown tools to finding a fixed point of the Hammerstein operator.
), we construct a quasi-measure of non-compactness and study its properties. Furthermore we prove the analog of the Darbo theorem using the measure of non-convexity. We also show the application of the shown tools to finding a fixed point of the Hammerstein operator.
2015-12-01 Nonlinear Seminar
Paweł Kliber
Consumer choices using hyperbolic discounting - the model and Euler conditions.
(Continuation of the 2015-11-17 Nonlinear Seminar)
2015-11-17 Nonlinear Seminar
Paweł Kliber
Consumer choices using hyperbolic discounting - the model and Euler conditions.
(Continuation of the 2015-10-20, 2015-11-03 and 2015-11-10 Nonlinear Seminar.)
2015-11-10 Nonlinear Seminar
Paweł Kliber
Consumer choices using hyperbolic discounting - the model and Euler conditions.
(Continuation of the 2015-10-20 and 2015-10-27 Nonlinear Seminar)
2015-11-03 Nonlinear Seminar
Paweł Kliber
Consumer choices using hyperbolic discounting - the model and Euler conditions.
(Continuation of the 2015-10-20 Nonlinear Seminar)
2015-10-27 Nonlinear Seminar
Elżbieta Gajecka
Resampling methods in the time domain for time series with periodic and almost periodic structure.
(The seminar will be held in room B3-38)
Statistical reasoning, in the case of time series, based on asymptotic distributions cannot always be a basis for effective statistical procedures. However unknown distributions of estimators or statistics can be approximated by the so-called resampling procedures. The idea of resampling methods is obtaining replications of the estimator and calculating the empirical distribution from those replications. The main question, to be answered, is whether this empirical distribution, called the resampling distribution, is close to the real distribution.
Intense research is being conducted towards resampling methods in nonstationary time series, in particular series with periodic and almost periodic structure. During this seminar various methods of resampling, especially subsampling, will be shown. The advantage of subsampling is its insensitivity to the shape of the asymptotic distribution. We will also show conditions of compatibility of resampling methods in the domain of time for 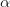 -mixing or weakly dependent time series with periodic or almost periodic structure. Especially weak dependency gives new tools to analyse statistical procedures for very general data generating time series, together with periodic series with long memory and heavy tails. An example of a periodic model with heavy tails and long memory will be shown.
-mixing or weakly dependent time series with periodic or almost periodic structure. Especially weak dependency gives new tools to analyse statistical procedures for very general data generating time series, together with periodic series with long memory and heavy tails. An example of a periodic model with heavy tails and long memory will be shown.
2015-10-20 Nonlinear Seminar
Paweł Kliber
Consumer choices using hyperbolic discounting - the model and Euler conditions.
This presentation concerns an article in which the problem of choosing the consumption path for a consumer using hyperbolic discounting (he treats the present and the whole future differently) in a model with random rate of return is discussed. The model, along with assumptions and the most important properties of the solution are presented.
2015-10-13 Nonlinear Seminar
Piotr Kasprzak
Abel's integral equation
(Continuation of the 2015-10-06 Nonlinear Seminar.)
2015-10-06 Nonlinear Seminar
Piotr Kasprzak
Abel's integral equation
The aim of the talk is to discuss mathematical background for the theory of Abel's integral equation and to present some of its real world applications.
2015-06-09 Nonlinear Seminar
Adam Nawrocki
Doubly periodic functions
(Continuation of the 2015-05-05 and 2015-04-28 Nonlinear Seminar)
2015-06-02 Nonlinear Seminar
Prof. Xiao-Xiong Gan
(Mathematics Department, Morgan State University, Baltimore, USA)
Some Remarks on Minkowski's Inequality
The classical Minkowski's inequality has two different forms based on the values of the positive number 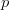 :
:
- If
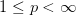 , then
, then 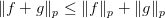 ;
; - If
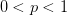 , then
, then 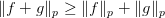 .
.
We provide a one-form Minkowski's inequality for all 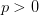 . A non-conjugate Hölder's inequality is also introduced. Some applications of the one-form Minkowski's inequality and non-conjugate Hölder's inequality are introduced too.
. A non-conjugate Hölder's inequality is also introduced. Some applications of the one-form Minkowski's inequality and non-conjugate Hölder's inequality are introduced too.
The lecture will be delivered in English
2015-05-19 Nonlinear Seminar
Patryk Kołacki
Sliding mode control in automatic control systems
(Continuation of the 2015-05-12 Nonlinear Seminar)
2015-05-12 Nonlinear Seminar
Patryk Kołacki
Sliding mode control in automatic control systems
In this seminar, I'm going to present you on the most popular control laws, i.e. sliding mode control. There will be discussed it's basic, canonical form and it's most popular applications. I also want to show a few examples which let you understand the idea of this control law.
2015-05-05 Nonlinear Seminar
Adam Nawrocki
Doubly periodic functions
(Continuation of the 2015-04-28 Nonlinear Seminar)
2015-04-28 Nonlinear Seminar
Adam Nawrocki
Doubly periodic functions
During this seminar we shall discuss the notion of doubly periodic functions and almost periodic functions in the context of elliptic functions.
2015-04-21 Nonlinear Seminar
dr Przemysław Chełminiak
What connects a biological cell with a partial diffusion equation.
Tracking individual molecules in living biological cells has become possible today by a new imaging technique called single-molecule spectroscopy. Interestingly, a diffusion of such tiny nano-molecules as proteins, nucleic acids or semiflexible polymers within a dense cellular environment is slower than ordinary Brownian diffusion of the micro-particles suspended in water. Their spatial development inside the cell, characterized by the time or ensemble averaged mean squared displacements, does not grow linearly in time. Moreover, these two averaging procedures are not equivalent when the measurement time is long compared to the characteristic time scale of the diffusion process. Therefore, the erratic motion of the subcellular molecules can not be perceived as a typical Brownian motion, but it must be considered in terms of the anomalous diffusion (subdiffusion). From a formal point of view, the anomalous diffusion can be described by a widely applicable stochastic process known as the continuous-time random walk model. We apply this method to construct the so called fractional Fokker-Planck equation which is an extended version of the subdiffusion equation in an external force field and close to thermal equilibrium. Using the methods of fractional calculus we find a few special solutions of this fractional partial differential equation and show that the mean squared displacement of a subdiffusing particle scales with time according to the power-law.
2015-04-14 Nonlinear Seminar
dr Giselle Monteiro
New convergence theorem for the abstract Kurzweil-Stieltjes integral
In theory of Riemann integral, the impact of the Bounded Convergence Theorem, also called Arzela or Arzela-Osgood or Osgood Theorem, is comparable to the importance of the Lebesgue Dominated convergence Theorem in the theory of the Lebesgue integration. In this talk we are concerned with the abstract Kurzweil-Stieltjes integral, that is, the Stieltjes type integral for functions with values in a Banach space introduced by S. Schwabik. Our aim is to present the Bounded Convergence Theorem in this general setting.
2015-03-31 Nonlinear Seminar
Piotr Maćkowiak
A combinatorial lemma ant it's consequences
(Continuation of the 2015-03-17 Nonlinear Seminar)
2015-03-24 Nonlinear Seminar
Marcin Borkowski
On a generalisation of a metric space
(Continuation of the 2015-03-10 Nonlinear Seminar)
2015-03-17 Nonlinear Seminar
Piotr Maćkowiak
A combinatorial lemma ant it's consequences
During this seminar we shall introduce a combinatorial lemma stating the existence for particular triangulations of the 202424.png) -dimensional simplex with a particular labeling of vertices of such triangulations with numbers
-dimensional simplex with a particular labeling of vertices of such triangulations with numbers 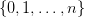 of a chain of simplices connecting a "vartex" with a "base" such that for any simplex from that chain each element of the set
of a chain of simplices connecting a "vartex" with a "base" such that for any simplex from that chain each element of the set 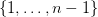 is a label of some vertex of that simplex. We shall show, that (simple) consequences of this lemma are:
is a label of some vertex of that simplex. We shall show, that (simple) consequences of this lemma are:
- the existence of zeros of the multidimensional function of excess demand
- the existence of continuum zeros of the parametrised multidimensional function of excess demand
- the well-known Sperner lemma
2015-03-10 Nonlinear Seminar
Marcin Borkowski
On a generalisation of a metric space
During this seminar we shall give the axioms of a 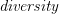 , which generalises the notion of metric spaces. We shall give examples of
, which generalises the notion of metric spaces. We shall give examples of 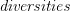 and prove some of their properties.
and prove some of their properties.
2015-03-03 Nonlinear Seminar
Jędrzej Sadowski
Quasicrystals and almost periodic patterns
(Continuation of the 2015-01-13, 2015-01-20 and 2015-01-27 Nonlinear Seminar)
2015-02-24 Nonlinear Seminar
dr Jacek Gulgowski
Compactness in spaces of functions of bounded variation.
The studies on the existence of fixed points of mappings in Banach spaces often involve methods connected with the Schauder fixed point theorem or the Leray-Schauder degree. Both approaches require the considered mappings to be completely continuous, and therefore, if one wants to work in spaces of functions of bounded variation, it is crucial to understand the mutual relations between 202424.png) and
and 202424.png) spaces. During the seminar we are going to discuss certain results on compact embeddings of such spaces and characterise the complete continuity of some nonlinear integral operators acting in
spaces. During the seminar we are going to discuss certain results on compact embeddings of such spaces and characterise the complete continuity of some nonlinear integral operators acting in 202424.png) spaces.
spaces.
2015-01-27 Nonlinear Seminar
Jędrzej Sadowski
Quasicrystals and almost periodic patterns
(Continuation of the 2015-01-13 and 2015-01-20 Nonlinear Seminar.)
2015-01-20 Nonlinear Seminar
Jędrzej Sadowski
Quasicrystals and almost periodic patterns
(Continuation of the 2015-01-13 Nonlinear Seminar.)
2015-01-13 Nonlinear Seminar
Jędrzej Sadowski
Quasicrystals and almost periodic patterns
During this seminar we shall introduce the definition of almost periodic patterns, their basic properties and connection to quasicrystals.
2014-12-09 Nonlinear Seminar
Monika Naskręcka
The existence of solutions of a certain system of differential equations with discontinuous right-hand side.
During this seminar we will discuss the existence of solutions of a certain system of differential equations with discontinuous right-hand side. This system depicts the dynamics of supplies in a model of competitive economy.
2014-12-02 Nonlinear Seminar
Marcin Borkowski
On a certain fixed point theorem for ultrametric spaces
We will discuss some variant of the Banach Contraction Principle, announced by N. Ackerman, for ultrametric spaces with metrics with values in a complete lattice.
(Continuation of the 2014-11-18 and 2014-11-04 Nonlinear Seminar.)
2014-11-25 Nonlinear Seminar
dr Przemysław Chełminiak
Stochastic dynamics of self-organizing critical nets
Self-organizing critical nets have been an object of intense research for over 15 years. They possess many peculiar properties, namely: fractality, self-similarity, topological criticality, little world effect and they are scale-free, which follow from their stochastic evolution. It occurs that many of such nets exist in an unstable state on the boundary of two phases, small-fractal world. Methods of construction and analysing critical nest will be shown, along with basic properties of probability distributions of stationary streams following stochastic dynamics of such nets.
2014-11-18 Nonlinear Seminar
Marcin Borkowski
On a certain fixed point theorem for ultrametric spaces
We will discuss some variant of the Banach Contraction Principle, announced by N. Ackerman, for ultrametric spaces with metrics with values in a complete lattice.
(Continuation of the 2014-11-04 Nonlinear Seminar.)
2014-11-04 Nonlinear Seminar
On a certain fixed point theorem for ultrametric spaces
We will discuss some variant of the Banach Contraction Principle, announced by N. Ackerman, for ultrametric spaces with metrics with values in a complete lattice.
2014-10-28 Nonlinear Seminar
Dr Mateusz Maciejewski
Existence of positive solutions of systems of parabolic equations with non-local initial conditions.
The topic of this speech is the existence of positive solutions of systems of parabolic equations with the boundary Dirichlet conditions and non-local initial conditions. For this purpose I shall show a fixed point theorem, which proof is based on Granas' fixed-point index. Thanks to the possibility of localisation of solutions I shall receive a theorem about existence of more than one solution.
2014-10-21 Nonlinear Seminar
Marcin Borkowski
Fixed point theorems with a boundary condition
2014-10-14 Nonlinear Seminar
Piotr Kasprzak
The game of Hex and the Brouwer fixed-point theorem.
During the seminar we are going to porve show that the celebrated Boruwer fixed-point theorem is a consequence of the fat that Hex cannot end in a draw.
2014-10-07 Nonlinear Seminar
Marcin Borkowski
Fixed point theorems with a boundary condition
In 1998, Espínola and López proved a certain fixed point theorem for a mapping transforming an admissible subset 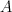 of a hyperconvex metric space into the whole space, assuming that this mapping sends the boundary of
of a hyperconvex metric space into the whole space, assuming that this mapping sends the boundary of 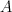 into
into 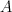 . We will show how to simplify their proof considerably, at the same time relaxing its assumptions. In particular, this will enable proving a new fixed point theorem, generalizing a classical result of Baillon from 1988.
. We will show how to simplify their proof considerably, at the same time relaxing its assumptions. In particular, this will enable proving a new fixed point theorem, generalizing a classical result of Baillon from 1988.
2014-09-30 Nonlinear Seminar
prof. Gennaro Infante
Nontrivial solutions of perturbed Hammerstein integral equations
We discuss the existence of positive solutions of some perturbed Hammerstein integral equations by means of classical fixed point index theory.We apply our results to some nonlocal BVPs that arise in some heat flow problems to prove the existence of multiple positive solutions under suitable conditions. We also illustrate how this approach might be applied to different problems.
2014-09-16 Nonlinear Seminar
Dariusz Bugajewski
BV-solutions of nonlinear equations
During the seminar we are going to prove the existence of BV-solutions to several nonlinear equations using the fixed point approach.
2014-06-10 Nonlinear Seminar
Adam Nawrocki
The convolution operator defined on the space of Levitan almost periodic functions.
(Continuation of the 2014-05-27 Nonlinear Seminar)
2014-05-27 Nonlinear Seminar
Adam Nawrocki
The convolution operator defined on the space of Levitan almost periodic functions.
It is known, that the convolution of a bounded, Levitan almost periodic function with a 202424.png) function is a bounded, Levitan almost periodic function. During this lecture we shall discuss the result we will receive when unbounded Levitan almost periodic functions are used.
function is a bounded, Levitan almost periodic function. During this lecture we shall discuss the result we will receive when unbounded Levitan almost periodic functions are used.
2014-05-20 Nonlinear Seminar
Adam Nawrocki
Asymptotic behaviour of a certain almost periodic function with regard to the Lebesgue measure
The function
3d5cfrac7b17d7b22b5ccos20x202b5ccos7b(x5csqrt202)7d7d0a205cend7bdisplaymath7d.png) (1)
(1)is a classical example of an unbounded and continuous
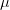 -almost periodic function. For this function we have
-almost periodic function. For this function we have7d7d3d0.0a205cend7bdisplaymath7d.png) (2)
(2)During this lecture we will discuss the idea of the proof of the equality above, which uses diophantic approximations. We shall furthermore show, that the limit
7d7d0a205cend7bdisplaymath7d.png) (3)
(3)does not exist.
2014-05-06 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2014-04-29, 2014-03-25, 2014-01-28, 2014-01-21, 2013-11-05 and 2013-10-29 Nonlinear Seminar)
2014-04-29 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2014-03-25, 2014-01-28, 2014-01-21, 2013-11-05
and 2013-10-29 Nonlinear Seminar)
2014-04-15 Nonlinear Seminar
Adam Nawrocki
Asymptotic behaviour of some 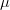 -almost periodic functions
-almost periodic functions
The function
3d5cfrac7b17d7b22b5ccos20x202b5ccos7b(x5csqrt202)7d7d0a205cend7bdisplaymath7d.png) (4)
(4)is a classical example of an unbounded and continuous
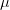 -almost periodic function. For this function we have
-almost periodic function. For this function we have7d7d3d0.0a205cend7bdisplaymath7d.png) (5)
(5)During this lecture we will consider if changing the number
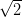 to another irrational number may have relevant impact on the behaviour of this function. We shall construct such a number
to another irrational number may have relevant impact on the behaviour of this function. We shall construct such a number 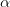 that the limit
that the limit7d7d0a205cend7bdisplaymath7d.png) (6)
(6)will not exist.
The lecture will be preceded by a short speech by Marcin Borkowski.
2014-04-01 Nonlinear Seminar
dr Michał Goliński
About some properties of the space of almost periodic functions
We will be talking about some properties of the space 202424.png) of the almost periodic functions, in particular the properties of the weak topology on this space (Cauchy sequences, completeness, reflexivity).
of the almost periodic functions, in particular the properties of the weak topology on this space (Cauchy sequences, completeness, reflexivity).
2014-03-25 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2013-10-29 and 2013-11-05 Nonlinear Seminar.)
2014-03-18 Nonlinear Seminar
Marcin Borkowski
On some application of Mönch theorem
(Continuation of the 2014-02-25 and 2014-03-04 Nonlinear Seminar.)
2014-03-11 Nonlinear Seminar
Dr Jacek Gulgowski
(Institute of Mathematics, Gdańsk University)
On the continuity of superposition operator in the spaces of functions of bounded variation
It is a well-know fact that the superposition of a function 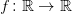 satisfying a local Lipschitz condition with a function
satisfying a local Lipschitz condition with a function 202424.png) of bounded variation leads to the function
of bounded variation leads to the function (t)202424.png) which is also of bounded variation. During the seminar we are going to present a few results concerning the continuity of such a superposition operator
which is also of bounded variation. During the seminar we are going to present a few results concerning the continuity of such a superposition operator ![$$ F \colon BV[0,1]\to BV[0,1] $$](https://octd.wmi.amu.edu.pl/latex/242420F205ccolon20BV5b02c15d5cto20BV5b02c15d202424.png) . Furthermore, we are going to discuss several generalizations of the concept of bounded variation in the sense of Jordan and investigate the issue of continuity of the superposition operator
. Furthermore, we are going to discuss several generalizations of the concept of bounded variation in the sense of Jordan and investigate the issue of continuity of the superposition operator ![$$ F \colon BV[0,1]\to E $$](https://octd.wmi.amu.edu.pl/latex/242420F205ccolon20BV5b02c15d5cto20E202424.png) , where
, where 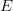 denotes the space of functions of bounded variation in the generalized sense.
denotes the space of functions of bounded variation in the generalized sense.
2014-03-04 Nonlinear Seminar
Marcin Borkowski
On some application of Mönch theorem.
(Continuation of the 2014-02-25 Nonlinear Seminar.)
2014-02-25 Nonlinear Seminar
Marcin Borkowski
On some application of Mönch theorem.
2014-01-28 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2014-01-21 Nonlinear Seminar)
2014-01-21 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2013-10-29 and 2013-11-05 Nonlinear Seminar)
2014-01-14 Nonlinear Seminar
prof. UW dr hab. Urszula Foryś (Warsaw University)
Modelling of biochemical reactions with delays
Nowadays, in the description of biochemical reactions not only ordinary differential equations but also equations with delays are applied. Time delays can be used to reflect different time scales at which modelled reactions occur. During our (together with M. Bodnarem, J. Miękisz and J. Poleszczuk) research we have found that simple, intuitive methods of introducing delay can lead to improper conclusions, such as oscillatory dynamics of the simple protein delayed degradation process. I shall show that the simplest model proposed by Bartsun et al. (2005) should be modified. It occurs that to obtain oscillatory dynamics one needs to consider much more complex reactions channel, with negative feedback and dimerization.
The seminar is to be held in room B1-37.
2014-01-07 Nonlinear Seminar
dr Aneta Sikorska-Nowak
Nonlinear Sturm – Liouville dynamic equation
Will be presented the necessary concepts of dynamic equations on time scales, and nonlinear dynamic equation of Sturm-Liouville.
2013-12-17 Nonlinear Seminar
Marcin Karczewski
Boltzmann kinetic equation
(Continuation of the 2013-12-10 Nonlinear Seminar)
2013-12-10 Nonlinear Seminar
Marcin Karczewski
Boltzmann kinetic equation
The aim of the seminar is to discuss the Boltzmann kinetic equation and its physical consequences. After gaining intuition we shall return to the earlier discussed VHP gas model.
2013-12-03 Nonlinear Seminar
Piotr Kasprzak
Application of formal power series to differential equations
During the seminar we are going to discuss the Frobenius Method, that is, we are going to seek solutions to certain differential equations (not necessarily of integer-order) in the form of formal power (or Laurent) series. Several illustrative examples will be provided.
2013-11-26 Nonlinear Seminar
dr Aneta Sikorska-Nowak
Asymptotic stability of the integro-differential equation with delay
(Continuation of the 2013-11-19 Nonlinear Seminar)
2013-11-19 Nonlinear Seminar
dr Aneta Sikorska-Nowak
Asymptotic stability of the integro-differential equation with delay
Certainly, the Lyapunov direct method has been, for more than 100 years, the main tool for the study of stability properties of ordinary, functional, integro-differential and partial differential equations. Nevertheless, the applications of this method to problem of stability in differential equations with delay has encountered serious difficulties if the delay is unbounded or if the equation has unbounded terms. The fixed point theory does not only solve the problem on stability but has a significant advantage over Lyapunov’s direct method.
I will present the results on the asymptotic stability of solutions of nonlinear integro-differential equations with delay using Sadovskii Fixed Point Theorem and properties of the measure of noncompactness.
2013-11-05 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
(Continuation of the 2013-10-29 Nonlinear Seminar)
2013-10-29 Nonlinear Seminar
Monika Naskręcka
Mathematical model of a competitive market with stocks.
Equilibrium and stability are the most frequently investigated properties in the market equilibrium models. On global and local markets we usually observe the lack of equilibrium. Nevertheless, the original model does not consider the possibility of stocks. However, we observe this situation, when there exists an excess supply. We should consider then how the accumulated stocks affect the equilibrium (or disequilibrium) and the stability of the model. During the seminar I will present the competitive economy model and the model with stocks. I will explore how these stocks influence the path of the price trajectory, equilibrium conditions and price stability.
2013-05-14 Nonlinear Seminar
Piotr Kasprzak
Application of formal power series to differential equations
(Continuation of the 2013-05-07 Nonlinear Seminar)
2013-05-07 Nonlinear Seminar
Piotr Kasprzak
Application of formal power series to differential equations
During the seminar we are going to discuss the Frobenius Method, that is, we are going to seek solutions to certain differential equations (not necessarily of integer-order) in the form of formal power (or Laurent) series. Several illustrative examples will be provided.
2013-04-23 Nonlinear Seminar
Dr. hab. Aleksander Ćwiszewski
TITLE soon
2013-04-09 Nonlinear Seminar
Prof. dr hab. Bronisław Jakubczyk (Institute of Mathematics, Polish Academy of Sciences)
Series of formally noncommutative variables versus functions and vector fields on manifolds
Taylor coefficients of a function can be calculated as iterated derivatives along constant vector fields (versors), computed at a fixed point. If a constant vector fields is replaced by any fixed set of vector fields on a manifold, a similar operation leads to the definition of a formal series with noncommutative variables.
We will show some interesting facts connected with such series, in particular the so-called realization theorem and its consequences. In particular, we will prove that a controlled and observed dynamical system on a manifold can be represented by such a series. Another consequence is a new test of convergence of a series of noncommutative variables.
2013-03-05 Nonlinear Seminar
Jędrzej Sadowski
About integrate-and-fire models
We will talk about two integrate-and-fire models.
The first one will be the neon bulb circuit, the second a japanese water toy.
2013-02-20 Nonlinear Seminar
Piotr Zdanowicz
Basic properties of formal series
During the seminar we will discuss and prove some properties of formal series.
(Continuation of the 2012-11-20 and 2012-11-27 Nonlinear Seminar)
2013-02-19 Nonlinear Seminar
Marcin Borkowski
Some properties of the Henstock-Kurzweil Integral
(Continuation of the 2013-01-22 and 2013-01-15 Nonlinear Seminar)
2013-01-22 Nonlinear Seminar
Marcin Borkowski
Some properties of the Henstock-Kurzweil Integral
(Continuation of the 2013-01-15 Nonlinear Seminar)
2013-01-15 Nonlinear Seminar
Marcin Borkowski
Some properties of the Henstock-Kurzweil Integral
During this seminar we will discuss some properties of the Henstock-Kurzweil Integral for an unbounded domain. In particular we shall prove that the functions of significantly bounded variation are multipliers of HK-integrable functions.
2013-01-08 Nonlinear Seminar
Monika Naskręcka
Homeomorphism of the space of polynomials and the space of their roots
(Continuation of the 2012-12-11 and 2012-12-18 Nonlinear Seminar)
2012-12-18 Nonlinear Seminar
Monika Naskręcka
Homeomorphism of the space of polynomials and the space of their roots
(Continuation of the 2012-12-11 Nonlinear Seminar)
2012-12-11 Nonlinear Seminar
Monika Naskręcka
Homeomorphism of the space of polynomials and the space of their roots
During this seminar an elementary, topological proof of continuity of the roots of complex polynomials with respect to their roots will be shown. For normed polynomials with complex coefficients and properly defined metric spaces this theorem can be expressed as a homeomorphism of corresponding metric spaces of coeffecients and roots.
2012-12-04 Nonlinear Seminar
Piotr Maćkowiak
The existence of surplus demand function zeros
(Continuation of the 2012-10-09 and 2012-10-16 Nonlinear Seminars.)
2012-11-27 Nonlinear Seminar
Piotr Zdanowicz
Basic properties of formal series
(Continuation of the 2012-11-20 Nonlinear Seminar)
2012-11-20 Nonlinear Seminar
Piotr Zdanowicz
Basic properties of formal series
2012-11-13 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of 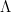 -bounded variation
-bounded variation
(Continuation of the 2012-10-30 Nonlinear Seminar)
2012-11-06 Nonlinear Seminar
The seminar will take place at 8:30 in the Faculty Council meeting room (A1-33/34)
Justyna Signerska
Firing map for integrate-and-fire models with an almost periodic drive
Consider the integrate-and-fire system 202424.png) ,
, 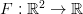 , in which the continuous dynamics is interrupted by the threshold-and-reset behaviour:
, in which the continuous dynamics is interrupted by the threshold-and-reset behaviour: 3dx_r202424.png) if
if 3dx_7b5cTheta7d202424.png) , meaning that once the value of a dynamical variable reaches a certain threshold
, meaning that once the value of a dynamical variable reaches a certain threshold 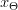 it is immediately reset to a resting value
it is immediately reset to a resting value 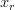 and the system evolves again according to the differential equation. The question is to describe the time series of consecutive resets (spikes)
and the system evolves again according to the differential equation. The question is to describe the time series of consecutive resets (spikes) 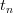 as iterations
as iterations 202424.png) of some map
of some map 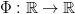 , called the firing map, and the sequence of interspike-intervals
, called the firing map, and the sequence of interspike-intervals 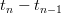 as a sequence of displacements
as a sequence of displacements -5cPhi5e7bn-17d(t_0)202424.png) along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.
along a trajectory of this map. The problem appears in various applications, e.g. in modelling of an action potential (spiking) by a neuron.
However, so far properties of the firing map were analytically investigated only for the function 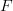 , which is smooth enough and often also periodic in
, which is smooth enough and often also periodic in 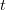 . We present a complete description of the properties of the firing map arising from the most popular models:
. We present a complete description of the properties of the firing map arising from the most popular models: 202424.png) (Leaky Integrate-and-Fire) and
(Leaky Integrate-and-Fire) and 202424.png) (Perfect Integrator), when the function
(Perfect Integrator), when the function  is only locally integrable and/or almost periodic. In particular, we prove that a Stepanov almost periodic function
is only locally integrable and/or almost periodic. In particular, we prove that a Stepanov almost periodic function  induces the firing map
induces the firing map 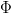 with the uniformly (Bohr) almost periodic displacement
with the uniformly (Bohr) almost periodic displacement 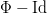 . In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.
. In this way we provide a formal framework for next studying of the interspike-intervals in almost-periodically driven integrate-and-fire models.
2012-10-30 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of 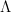 -bounded variation
-bounded variation
During the seminar we are going to define a certain class of functions of 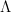 -bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
-bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
2012-10-23 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of 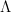 -bounded variation
-bounded variation
During the seminar we are going to define a certain class of functions of 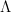 -bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
-bounded variation and prove some properties of such functions. Furthermore, we are going to show that endowed with a certain functional the class in questions becomes a strictly convex Banach space. We are also going to provide several non-trivial examples illustrating our considerations.
2012-10-16 Nonlinear Seminar
Piotr Maćkowiak
The existence of surplus demand function zeros
(Continuation of the 2012-10-09 Nonlinear Seminar)
2012-10-09 Nonlinear Seminar
Piotr Maćkowiak
The existence of surplus demand function zeros
2012-05-29 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of bounded variation
(Continuation of the 2012-04-24 Nonlinear Seminar)
2012-05-22 Nonlinear Seminar
Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
(Continuation of the 2012-05-08 Nonlinear Seminar)
2012-05-15 Nonlinear Seminar
Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
(Continuation of the 2012-05-08 Nonlinear Seminar)
2012-05-08 Nonlinear Seminar
Michał Burzyński
Alternative proofs of Arrow's impossibility theorem
Arrow's impossibility theorem states, that if there are at least three potential social states, there is no such social welfare function  (that describes the society as a whole with given individual preferences), which satisfies the following four conditions:
(that describes the society as a whole with given individual preferences), which satisfies the following four conditions:  has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle;
has an unbounded domain; the strong relation of social preferences satisfies the weak Pareto principle;  satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function
satisfies the property of independence of irrelevant alternatives and in a society with preferences described with the function  there is no dictatorship. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.
there is no dictatorship. The original proof, given by K. Arrow, consists of two steps: to show the existence of a deciding unit and to prove, it must be a dictator. The first of the alternative proofs is based on using the Condorcet preference. The second proof applies the first step of Arrow's proof and points, that all social decisions are made in the same way. The last proof is of graphic character.
2012-04-24 Nonlinear Seminar
Piotr Kasprzak
On a certain class of functions of bounded variation
We are going to define a relatively large class of functions of bounded variation defined on an open subset of 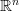 , which in particular contains the Sobolev space
, which in particular contains the Sobolev space 202424.png) . Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.
. Furthermore, we are going to discuss the connection between the classical variation in the sense of Jordan and the generalized one.
2012-04-03 Nonlinear Seminar
Piotr Kasprzak
On the compactness criterion in the space of bounded real-valued continuous functions defined on a non-compact domain
During the seminar we are going to discuss a certain compactness criterion in the space of bounded real-valued continuous functions defined on a non-compact domain related to the well-known Arzela-Ascoli theorem.
2012-03-27 Nonlinear Seminar
Piotr Maćkowiak
Exploding points
We will present and prove theorem of the exploding point. This theorem states that for any function defined on a compact set X, containing the cube K centered at zero in its interior, with values in X\K, which is the identity on the boundary of the set X, there exists a point c in X, that in any surroundings of c, there is a point x such that the value of f(x) and f(c) are located on opposite walls of the cube K.
2012-03-20 Nonlinear Seminar
Adam Nawrocki
An Application of Continued Fractions
During this seminar we will discuss basic properties of Continued Fractions. Next we shall use Continued Fractions to calculate the limit of:2b5ccos(5csqrt7b27dx)7d202424.png)
(Continuation of the 2012-03-13 Nonlinear Seminar)
2012-03-13 Nonlinear Seminar
Adam Nawrocki
An Application of Continued Fractions
During this seminar we will discuss basic properties of Continued Fractions. Next we shall use Continued Fractions to calculate the limit of:2b5ccos(5csqrt7b27dx)7d202424.png)
2012-03-06 Nonlinear Seminar
Marcin Wachowiak
Applications of Theorem Hopf-Lefschetz fixed point
(Continuation of the 2011-11-22 Nonlinear Seminar and 2011-11-29 Nonlinear Seminar and 2011-12-06 Nonlinear Seminar).
2012-02-28 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar, 2012-01-03 Nonlinear Seminar, 2012-02-14 Nonlinear Seminar and 2012-02-21 Nonlinear Seminar).
2012-02-21 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar and 2012-01-03 Nonlinear Seminar and 2012-02-14 Nonlinear Seminar).
2012-02-14 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar and 2012-01-03 Nonlinear Seminar).
2012-01-24 Nonlinear Seminar
Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
(Continuation of the 2012-01-10 Nonlinear Seminar and 2012-01-17 Nonlinear Seminar).
2012-01-17 Nonlinear Seminar
Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
(Continuation of the 2012-01-10 Nonlinear Seminar).
2012-01-10 Nonlinear Seminar
Daria Bugajewska
On differential and inetgral equations in the spaces of functions of Lambda-bounded variation.
We are going to consider linear differential and nonlinear integral equations in the
spaces of functions of Lambda-bounded variation. We will state the existence and the existence and uniqueness results in this space as well as in its subspace consisting of contninuous functions of Lambda-bounded variation.
2012-01-03 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
(Continuation of the 2011-12-20 Nonlinear Seminar).
2011-12-20 Nonlinear Seminar
Jędrzej Sadowski
Definitions of the N-almost periodic functions
We will show differend ways to define N-almost periodic functions and prove their equivalence.
2011-12-13 Nonlinear Seminar
Marcin Wachowiak
Applications of Theorem Hopf-Lefschetz fixed point
(Continuation of the 2011-11-22 Nonlinear Seminar and 2011-11-29 Nonlinear Seminar and 2011-12-06 Nonlinear Seminar).
2011-12-06 Nonlinear Seminar
Marcin Wachowiak
Applications of Theorem Hopf-Lefschetz fixed point
(Continuation of the 2011-11-22 Nonlinear Seminar and 2011-11-29 Nonlinear Seminar).
2011-11-29 Nonlinear Seminar
Marcin Wachowiak
Applications of Theorem Hopf-Lefschetz fixed point
(Continuation of the 2011-11-22 Nonlinear Seminar).
2011-11-22 Nonlinear Seminar
Marcin Wachowiak
Applications of Theorem Hopf-Lefschetz fixed point
In the first part of the discussion we introduce the necessary concepts and facts about the homology and cohomology, then we will discuss the Hopf-Lefschetz theorem and its applications
2011-11-15 Nonlinear Seminar
Marcin Borkowski, Piotr Maćkowiak (Poznań University of Economics)
On superposition of formal power series
(Continuation of the 2011-11-08 Nonlinear Seminar)
2011-11-08 Nonlinear Seminar
Marcin Borkowski, Piotr Maćkowiak (Poznań University of Economics)
On superposition of formal power series
We will present a new proof of a criterion for existence of superposition of formal power series given by Gan and Knox. We will also give some properties concerning the behavior of such series on the boundary of their convergence circle.
2011-10-25 Nonlinear Seminar
Adam Burchardt
Schauder fixed point, revisited
(Continuation of the 2011-10-18, 2011-10-11 and 2011-10-04 nonlinear seminars).
2011-10-18 Nonlinear Seminar
Adam Burchardt
Schauder fixed point, revisited
(Continuation of the 2011-10-11 and 2011-10-04 nonlinear seminars).
2011-10-11 Nonlinear Seminar
Adam Burchardt
Schauder fixed point, revisited
(Continuation of the 2011-10-04 Nonlinear Seminar).
2011-10-04 Nonlinear Seminar
Adam Burchardt
Schauder fixed point, revisited
During the seminar we are going to discuss the following generalization of the classical Schauder fixed point theorem due to R. Cauty:
Let 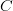 be a convex subset of a topological vector space
be a convex subset of a topological vector space 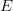 . If
. If 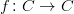 is a continuous function such that
is a continuous function such that 202424.png) is contained in a compact subset of
is contained in a compact subset of 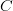 , then
, then  has a fixed point.
has a fixed point.
The talk is based on the following paper: R. Cauty, Solution du problème de point fixe de Schauder, Fund. Math. 170 (2001), 231-246.
2011-06-14 Nonlinear Seminar
Marcin Borkowski
Some remarks on convergence of power series at the boundary of the convergence circle
We will present a theorem concerning convergence of power series—together with all its derivatives—at the boundary of the convergence circle.
2011-05-24 Nonlinear Seminar
Joanna Wypych
On superposition of formal power series
(Continuation of the 2011-05-10 and 2011-05-17 seminars)
2011-05-17 Nonlinear Seminar
Joanna Wypych
On superposition of formal power series
(Continuation of the 2011-05-10 Nonlinear Seminar)
2011-05-10 Nonlinear Seminar
Joanna Wypych
On superposition of formal power series
In the beginning we will present basic definitions concerning formal power series and their properties. Then we will discuss two theorems on superposition of such series. The talk is based on a paper On composition of formal power series by Xiao-Xiong Gan and Nathaniel Knox.
2011-04-19 Nonlinear Seminar
Piotr Kasprzak
On the equivalent characterizations of Levitan almost periodic functions
(Continuation of the 2011-02-22 Nonlinear Seminar)
2011-04-12 Nonlinear Seminar
Marcin Borkowski
On formal power series
(Continuation of the 2010-12-21 and 2011-03-15 Nonlinear Seminar seminars)
2011-04-05 Nonlinear Seminar
Adam Nawrocki
Examples of Henstock-Kurzweil integrable functions
We will present methods of proving Henstock-Kurzweil integrability of real functions.
2011-03-29 Nonlinear Seminar
Piotr Kasprzak
On a new class of almost periodic functions
During the talk not only will we define the so-called quasi almost automorphic functions but also we will prove some basic properties of these functions.
2011-03-22 Nonlinear Seminar
Joanna Wypych
Formal power series
(Continuation of the 2011-01-18 and 2011-03-08 seminars)
2011-03-15 Nonlinear Seminar
Marcin Borkowski
On formal power series
(Continuation of the 2010-12-21 Nonlinear seminar).
2011-03-08 Nonlinear Seminar
Joanna Wypych
Formal power series
(Continuation of the 2011-01-18 Nonlinear Seminar)
2011-03-01 Nonlinear Seminar
On the dual space to the space of Henstock-Kurzweil integrable functions
During the talk we will present the result of Alexiewicz which gives a characterization of the dual space to the space of Henstock-Kurzweil integrable functions defined on a bounded interval.
2011-02-22 Nonlinear Seminar
Piotr Kasprzak
On the equivalent characterizations of Levitan almost periodic functions
2011-01-18 Nonlinear Seminar
Joanna Wypych
Formal power series
We will discuss basic properties of formal power series and the Krull topology. Among others, we will present theorems on the distributive laws and invertibility of a series. The talk will be based on the book by S. Łojasiewicz and J. Stasica Formal analysis and analytic functions (in Polish).
2011-01-11 Nonlinear Seminar
Marcin Wachowiak
A fixed point theorem for mappings satisfying the interior condition
(Continuation of the 2010-11-23, 2010-11-30 and 2010-12-07 Nonlinear seminars).
2011-01-04 Nonlinear Seminar
Wojciech Jankowski
On a certain fixed point theorem for discontinuous mappings
2010-12-21 Nonlinear Seminar
Marcin Borkowski
On formal power series
The aim of the talk is to give an introduction into the theory of formal power series. After the basic definitions and properties we will show some application to combinatorics. Finally, we will show an example of a formal differential equation.
2010-12-14 Nonlinear Seminar
On the compactness criterion in the space of bounded real-valued continuous functions defined on a non-compact domain