Xiao-Xiong Gan (Morgan State University, Baltimore MD, USA)
From Formal Power Series to Formal Analysis
For any 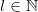 , a formal power series on a ring
, a formal power series on a ring 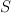 is defined to be a mapping from
is defined to be a mapping from 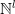 to
to 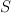 . A formal power series
. A formal power series  in
in  from
from 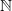 to
to 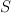 is usually denoted as a sequence
is usually denoted as a sequence 202424.png) or as a power series
or as a power series 203d20a_0202b20a_120z202b205ccdots202b20a_n20z5en202b205ccdots202424.png) , where
, where 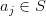 for every
for every 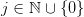 . The set of all formal power series on
. The set of all formal power series on 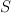 is denoted by
is denoted by 202424.png) .
.
If considering a formal power series as a sequence, what is the difference between 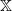 and
and 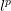 ?
?
If considering a formal power series as a power series, what is the difference between formal power series and the traditional power series? What is the relationship between formal power series and traditional power series?
What is formal analysis?
This talk tries to answer those questions and brings discussion of all kinds of questions about formal analysis, a relatively new mathematical subject.