Piotr Maćkowiak
Continuity of the non-autonomous superposition operator and around
We shall present an example of a function ![$$ f:[0,1]\times\mathbb R\to \mathbb R $$](http://octd.wmi.amu.edu.pl/latex/242420f3a5b02c15d5ctimes5cmathbb20R5cto205cmathbb20R202424.png)
which is lipschitzian and such that the (non-autonomous) superposition operator it generates is not continuous (as a mapping from 
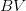to 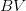). We shall show necessary and sufficient conditions for a non-autonomous superposition operator to be continuous (in 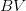). We shall also prove some results for 
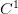-class generators.